Every year thousands of students are graduating but the placement strategies of recruiters have varied completely. This makes the students work harder to get jobs in tech companies. We understand this hustle, and that's why we bring to you the most informative tech blogs to ace your placement interviews.
Today's blog is about pattern matching using a new algorithm called Boyer-Moore Algorithm. Here, we'll gain in-depth knowledge about the algorithm and the strategies used, along with their implementation in C++, Python, and Java. So, let's get started!
What is Boyer-Moore Algorithm?
In the year 1977, Robert Boyer and J Strother Moore established an algorithm that proved to be very effective for the various pattern-searching problems in the computing world. They named it the Boyer-Moore algorithm which has served as the benchmark for pattern-searching algorithms ever since.
Unlike the traditional way of pattern searching where we try to match the two strings in a forward manner, the Boyer-Moore advances the concept by beginning to match the last character of the string to be searched. In this way, the time complexity is reduced significantly.
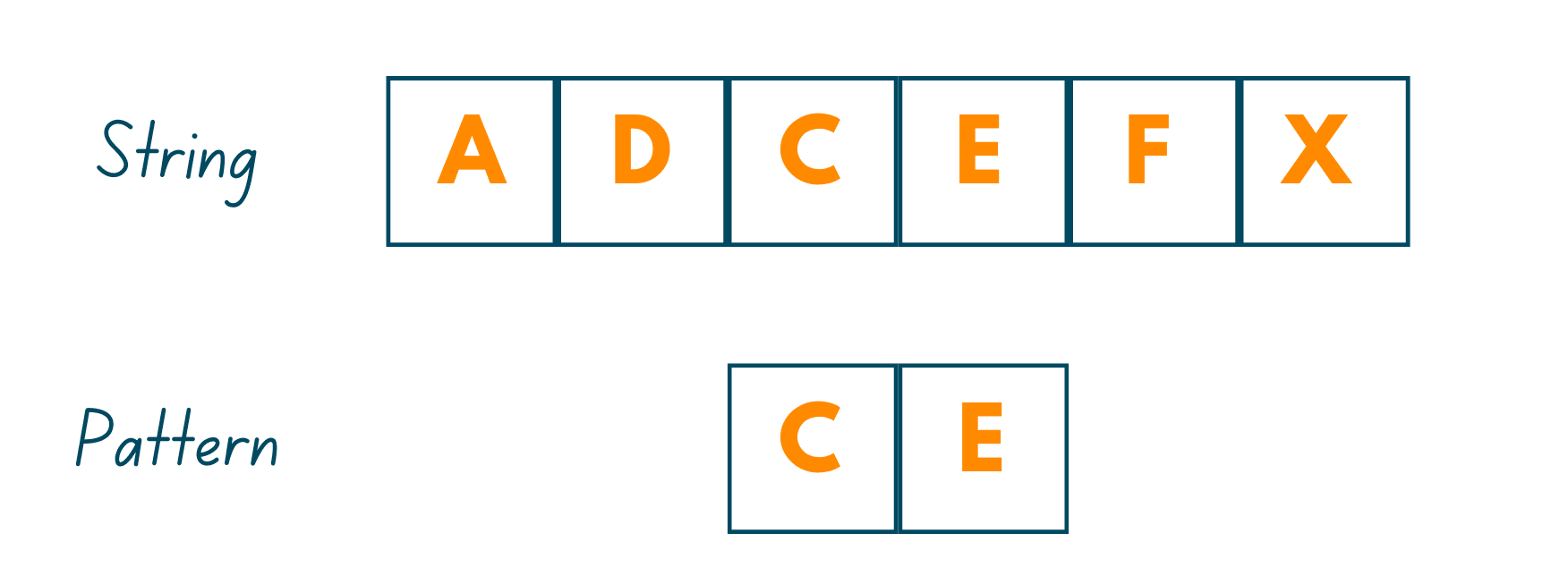
As mentioned earlier, this algorithm takes the backward approach by aligning the pattern string P with text string T and thereafter, comparing the characters from right to left, starting with the rightmost character. It works on the principle that if a mismatched character is found, then there is no use in matching the other characters in the two strings.
To work effectively, there are two strategies/approaches we use in this algorithm:
- Bad Character Heuristics
- Good Suffix Heuristics
In the following, we have explained in detail both the strategies along with their implementation in C++, Java, and Python.
01) Bad Character Heuristics
This intuition behind solving the pattern-matching problem is quite simple. Just as its name suggests, here, the first character that we encounter which does not match the pattern we are searching for, is called the Bad Character. On encountering the bad character, we:
Case I: Shift the pattern till the mismatch becomes a match
As mentioned earlier, we start checking the pattern occurrence from the rightmost character, so in this case, we'll find the bad character. Now, we'll shift the pattern in such a way that it gets aligned with the mismatched character in the text. For more clarity, you can see the illustration:
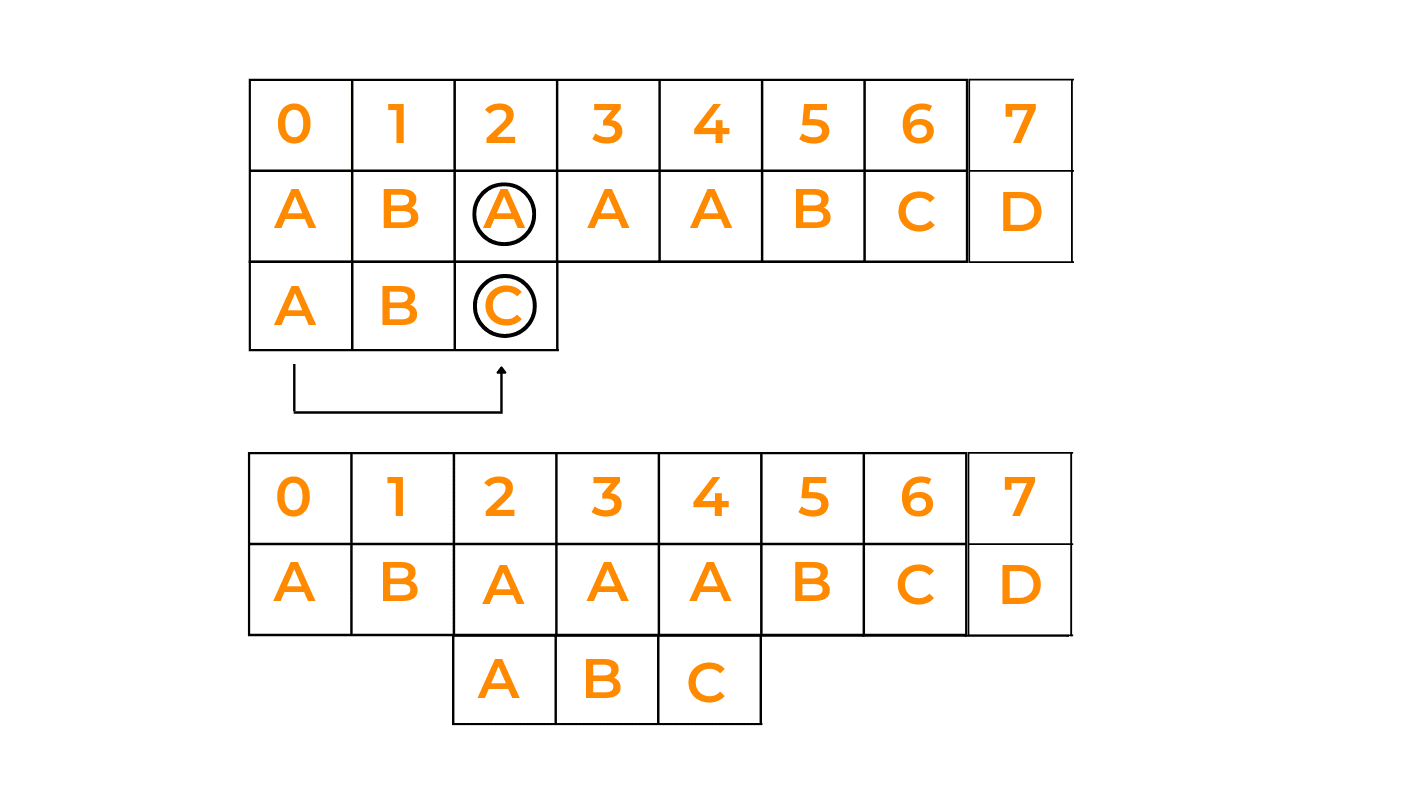
Explanation: As we have already stated that in this algorithm, the matching begins from the rightmost character. So, we start matching the text with the pattern. On matching the first character of the pattern we observe that 'C' does not match with 'A'. So, we try to match the 'A' of the given text with 'A'(if present) in the pattern. So, we shift the pattern by 2 so that the rightmost character of both strings matches. Thereafter, we match the other 2 characters.
Case II: Shift the pattern till it moves past the bad character
In this case, we'll begin matching the pattern from the right end, and see if it matches one by one with all the characters of the given string. If at any time, we observe that the rightmost character is not matching with the rightmost character of the given string, we shift the whole pattern ahead of the last character of the string with which we were trying to match the pattern. Have a look at the below image:
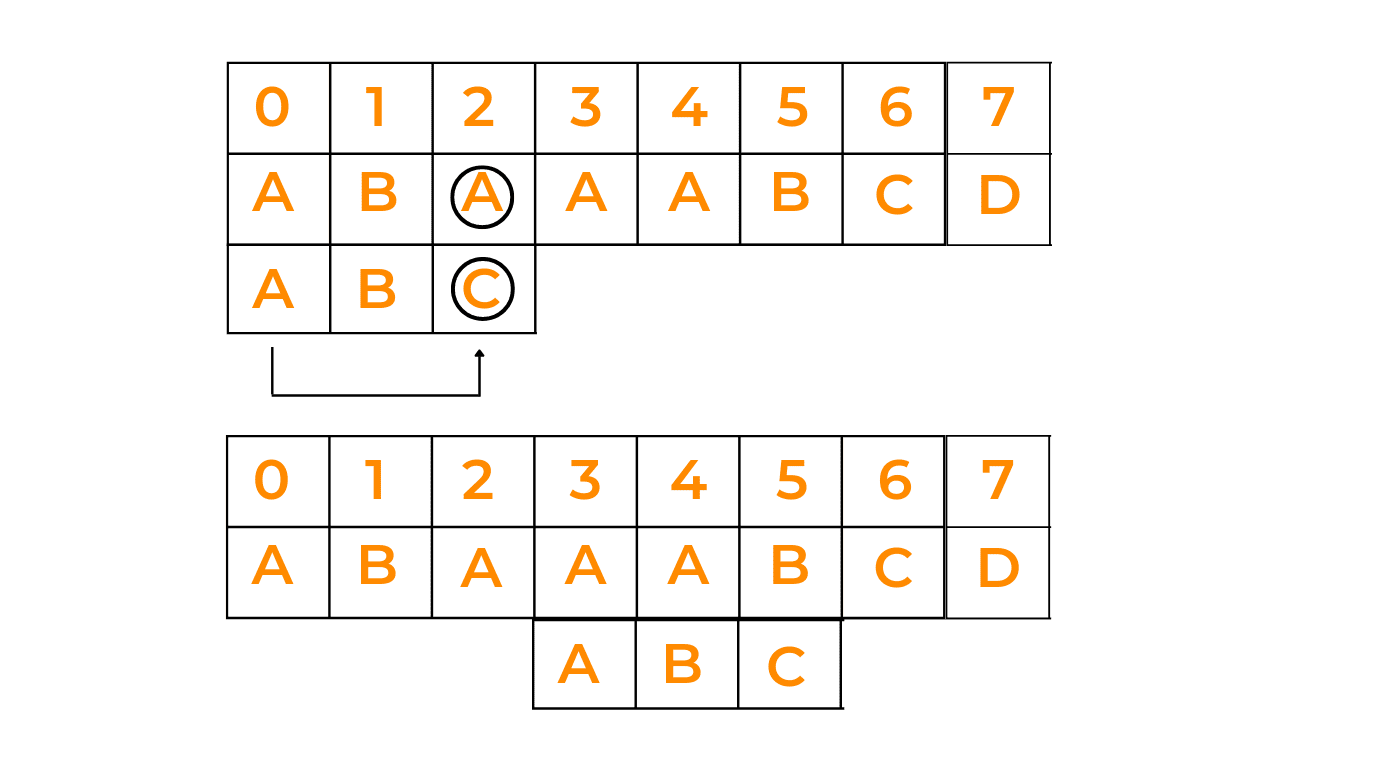
Explanation: Now, in this case, observe that we have a mismatch at character 'C'. Now, after going through the whole pattern, we observe that it does not contain any 'C'. So, we take the whole pattern and move it right across the letter 'C' and later, check for it to match.
Implementation of Bad Character Heuristics (Boyer-Moore) in C++
#include <bits/stdc++.h> using namespace std; # define NO_OF_CHARS 256 void badCharHeuristic( string str, int size, int badchar[NO_OF_CHARS]) { int i; // Initializing all occurrences as -1 for (i = 0; i < NO_OF_CHARS; i++) badchar[i] = -1; // Fill the actual value of last occurrence // of a character for (i = 0; i < size; i++) badchar[(int) str[i]] = i; } void search( string txt, string pat) { int m = pat.size(); int n = txt.size(); int badchar[NO_OF_CHARS]; /* Fill the bad character array by calling the preprocessing function badCharHeuristic() for given pattern */ badCharHeuristic(pat, m, badchar); int s = 0; while(s <= (n - m)) { int j = m - 1;
/* Keep reducing index j of pattern while characters of pattern and text are matching at this shift s */ while(j >= 0 && pat[j] == txt[s + j]) j--; /* If the pattern is present at current shift, then index j will become -1 after the above loop */ if (j < 0) { cout << "pattern occurs at shift = " << s << endl; s += (s + m < n)? m-badchar[txt[s + m]] : 1; } else s += max(1, j - badchar[txt[s + j]]); } } /* Driver code */ int main() { string txt= "ABAAABCD"; string pat = "ABC"; search(txt, pat); return 0; }
Implementation of Bad Character Heuristics (Boyer-Moore) in Python
NO_OF_CHARS = 256 def badCharHeuristic(string, size): # Initialize all occurrence as -1 badChar = [-1]*NO_OF_CHARS # Fill the actual value of last occurrence for i in range(size): badChar[ord(string[i])] = i; # return initialized list return badChar def search(txt, pat): m = len(pat) n = len(txt) # create the bad character list by calling # the preprocessing function badCharHeuristic() # for given pattern badChar = badCharHeuristic(pat, m) # s is shift of the pattern with respect to text s = 0 while(s <= n-m): j = m-1 # Keep reducing index j of pattern while # characters of pattern and text are matching # at this shift s while j>=0 and pat[j] == txt[s+j]: j -= 1 # If the pattern is present at current shift, # then index j will become -1 after the above loop if j<0: print("Pattern occur at shift = {}".format(s)) s += (m-badChar[ord(txt[s+m])] if s+melse 1) else: s += max(1, j-badChar[ord(txt[s+j])])
def main(): txt = "ABAAABCD" pat = "ABC" search(txt, pat) if __name__ == '__main__': main()
Implementation of Bad Character Heuristics(Boyer-Moore) in Java
class Solution{ static int NO_OF_CHARS = 256;
static int max (int a, int b) { return (a > b)? a: b; } //returns max of two numbers
static void badCharHeuristic( char []str, int size,int badchar[]) { // Initialize all occurrences as -1 for (int i = 0; i < NO_OF_CHARS; i++) badchar[i] = -1; // Fill the actual value of last occurrence of a character for (int i = 0; i < size; i++) badchar[(int) str[i]] = i; } static void search( char txt[], char pat[]) { int m = pat.length; int n = txt.length; int badchar[] = new int[NO_OF_CHARS];
badCharHeuristic(pat, m, badchar); int s = 0; while(s <= (n - m)) { int j = m-1; /* Keep reducing index j of pattern while characters of pattern and text are matching at this shift s */ while(j >= 0 && pat[j] == txt[s+j]) j--; /* If the pattern is present at current shift, then index j will become -1 after the above loop */ if (j < 0) { System.out.println("Patterns occur at shift = " + s); s += (s+m < n)? m-badchar[txt[s+m]] : 1; } else s += max(1, j - badchar[txt[s+j]]); } } public static void main(String []args) { char txt[] = "ABAAABCD".toCharArray(); char pat[] = "ABC".toCharArray(); search(txt, pat); } }
Output:
Pattern occurs at 4
02) Good Suffix Heuristics
Just like in the Bad Character approach preprocessing is done, in this strategy also, preprocessing is done based on certain scenarios. Here, we have 3 different cases that will tell which step we need to follow next to match the given pattern efficiently:
Case I: Shift the pattern until the next occurrence is found
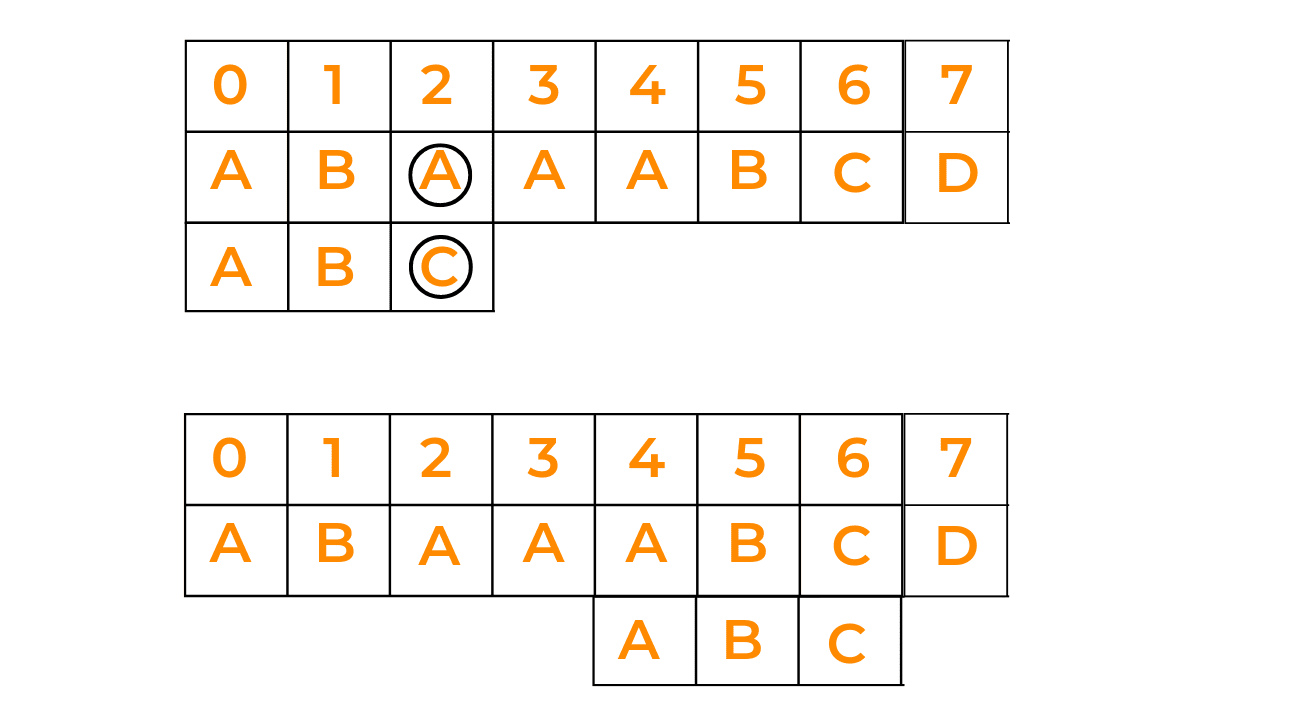
Here, when we see that pattern is not matching with the given string, we shift the pattern to the right side to check whether that pattern is present in the further characters of the string. See the given image:
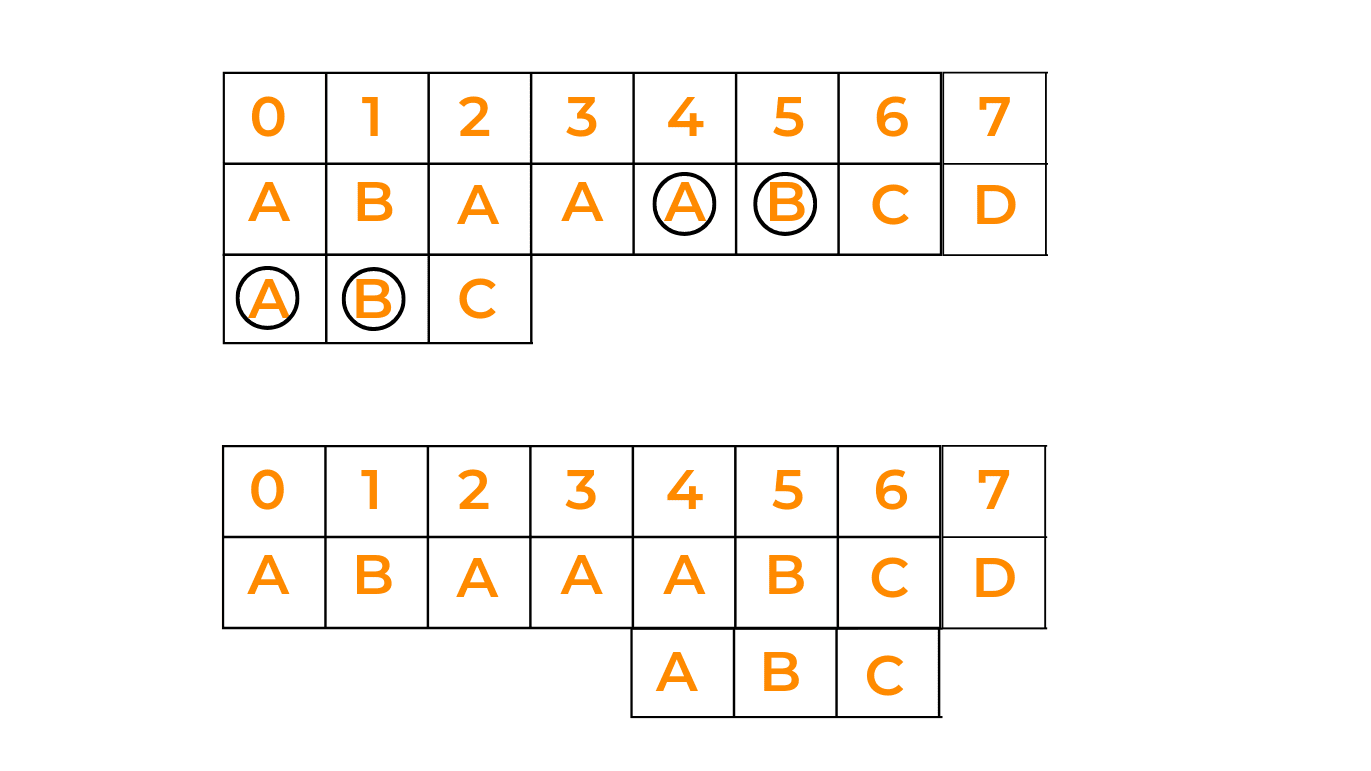
Case II: Shift pattern till prefix of pattern matches with a suffix of text
In this case, if we're not able to find the pattern in one go, we try to match the prefix of the pattern with a possible suffix of the given text, by shifting the pattern that many times as the length of the prefix. Have a look at the given image:
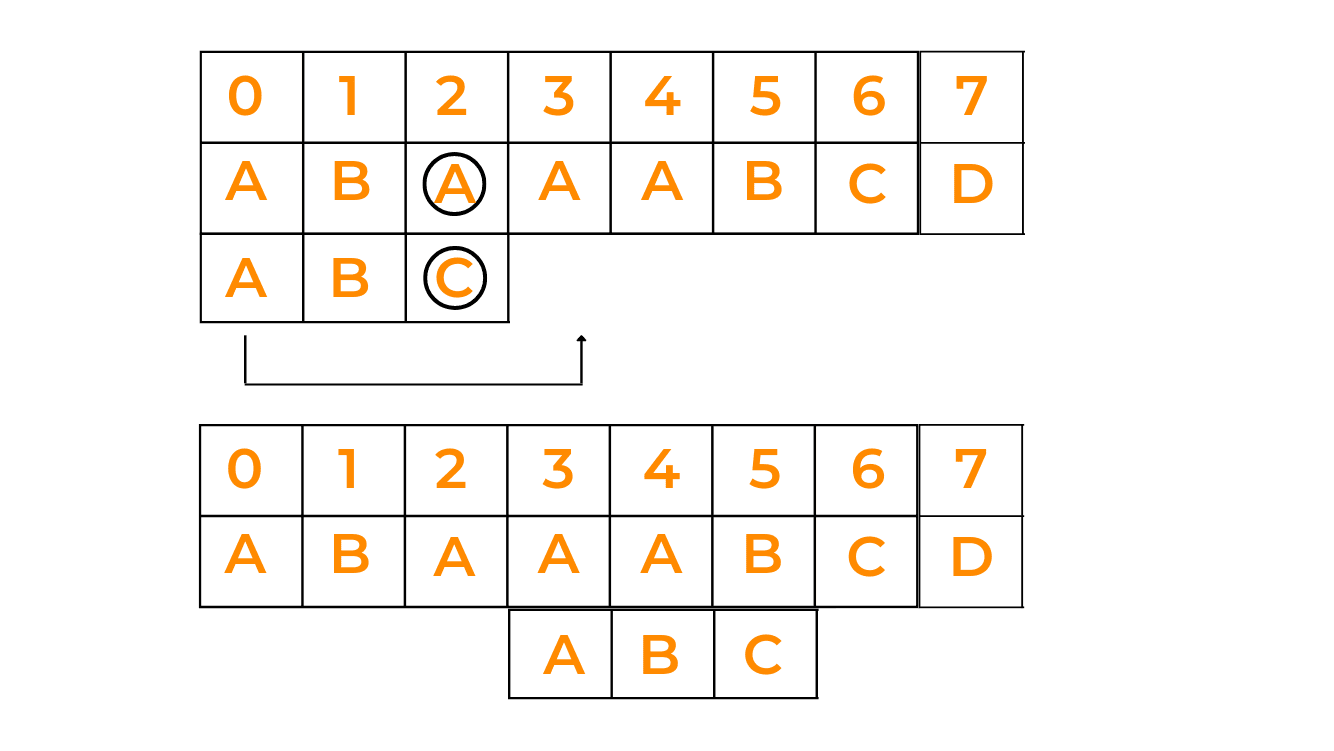
Case III: Shift pattern till the pattern moves past the provided text
This happens when there is no possibility of the pattern matching with the string. In this case, we just shift the pattern till the end. Look at the given illustration:
Implementation of Good Suffix Heuristics(Boyer-Moore) with C++
/* C program for Boyer Moore Algorithm with Good Suffix heuristic to find pattern in given text string */ #include #include // preprocessing for strong good suffix rule void preprocess_strong_suffix(int *shift, int *bpos, char *pat, int m) { // m is the length of pattern int i=m, j=m+1; bpos[i]=j; while(i>0) { /*if character at position i-1 is not equivalent to character at j-1, then continue searching to right of the pattern for border */ while(j<=m && pat[i-1] != pat[j-1]) { /* the character preceding the occurrence of t in pattern P is different than the mismatching character in P, we stop skipping the occurrences and shift the pattern from i to j */ if (shift[j]==0) shift[j] = j-i; //Update the position of next border j = bpos[j]; } /* p[i-1] matched with p[j-1], border is found. store the beginning position of border */ i--;j--; bpos[i] = j; } } //Preprocessing for case 2 void preprocess_case2(int *shift, int *bpos, char *pat, int m) { int i, j; j = bpos[0]; for(i=0; i<=m; i++) { /* set the border position of the first character of the pattern to all indices in array shift having shift[i] = 0 */ if(shift[i]==0) shift[i] = j; /* suffix becomes shorter than bpos[0], use the position of next widest border as value of j */ if (i==j) j = bpos[j]; } } /*Search for a pattern in given text using Boyer Moore algorithm with Good suffix rule */ void search(char *text, char *pat) { // s is shift of the pattern with respect to text int s=0, j; int m = strlen(pat); int n = strlen(text); int bpos[m+1], shift[m+1]; //initialize all occurrence of shift to 0 for(int i=0;i<m+1;i++) shift[i]=0; //do preprocessing preprocess_strong_suffix(shift, bpos, pat, m); preprocess_case2(shift, bpos, pat, m); while(s <= n-m) { j = m-1; /* Keep reducing index j of pattern while characters of pattern and text are matching at this shift s*/ while(j >= 0 && pat[j] == text[s+j]) j--; /* If the pattern is present at the current shift, then index j will become -1 after the above loop */ if (j<0) { printf("pattern occurs at shift = %d\n", s); s += shift[0]; } else /*pat[i] != pat[s+j] so shift the pattern shift[j+1] times */ s += shift[j+1]; } } //Driver int main() { char text[] = "ABAAAABAACD"; char pat[] = "ABA"; search(text, pat); return 0; }
Implementation of Good Suffix Heuristics(Boyer-Moore) with Python
# Python3 program for Boyer Moore Algorithm with # Good Suffix heuristic to find pattern in # given text string # preprocessing for strong good suffix rule def preprocess_strong_suffix(shift, bpos, pat, m): # m is the length of pattern i = m j = m + 1 bpos[i] = j while i > 0: '''if character at position i-1 is not equivalent to character at j-1, then continue searching to right of the pattern for border ''' while j <= m and pat[i - 1] != pat[j - 1]: ''' the character preceding the occurrence of t in pattern P is different than the mismatching character in P, we stop skipping the occurrences and shift the pattern from i to j ''' if shift[j] == 0: shift[j] = j - i # Update the position of next border j = bpos[j] ''' p[i-1] matched with p[j-1], border is found. store the beginning position of border ''' i -= 1 j -= 1 bpos[i] = j # Preprocessing for case 2 def preprocess_case2(shift, bpos, pat, m): j = bpos[0] for i in range(m + 1): ''' set the border position of the first character of the pattern to all indices in array shift having shift[i] = 0 ''' if shift[i] == 0: shift[i] = j ''' suffix becomes shorter than bpos[0], use the position of next widest border as value of j ''' if i == j: j = bpos[j] '''Search for a pattern in given text using Boyer Moore algorithm with Good suffix rule ''' def search(text, pat): # s is shift of the pattern with respect to text s = 0 m = len(pat) n = len(text) bpos = [0] * (m + 1) # initialize all occurrence of shift to 0 shift = [0] * (m + 1) # do preprocessing preprocess_strong_suffix(shift, bpos, pat, m) preprocess_case2(shift, bpos, pat, m) while s <= n - m: j = m - 1 ''' Keep reducing index j of pattern while characters of pattern and text are matching at this shift s''' while j >= 0 and pat[j] == text[s + j]: j -= 1 ''' If the pattern is present at the current shift, then index j will become -1 after the above loop ''' if j < 0: print("pattern occurs at shift = %d" % s) s += shift[0] else: '''pat[i] != pat[s+j] so shift the pattern shift[j+1] times ''' s += shift[j + 1] # Driver Code if __name__ == "__main__": text = "ABAAAABAACD" pat = "ABA" search(text, pat)
Implementation of Good Suffix Heuristics(Boyer-Moore) with Java
/* Java program for Boyer Moore Algorithm with Good Suffix heuristic to find pattern in given text string */ class GFG { // preprocessing for strong good suffix rule static void preprocess_strong_suffix(int []shift, int []bpos, char []pat, int m) { // m is the length of pattern int i = m, j = m + 1; bpos[i] = j; while(i > 0) { /*if character at position i-1 is not equivalent to character at j-1, then continue searching to right of the pattern for border */ while(j <= m && pat[i - 1] != pat[j - 1]) { /* the character preceding the occurrence of t in pattern P is different than the mismatching character in P, we stop skipping the occurrences and shift the pattern from i to j */ if (shift[j] == 0) shift[j] = j - i; //Update the position of next border j = bpos[j]; } /* p[i-1] matched with p[j-1], border is found. store the beginning position of border */ i--; j--; bpos[i] = j; } } //Preprocessing for case 2 static void preprocess_case2(int []shift, int []bpos, char []pat, int m) { int i, j; j = bpos[0]; for(i = 0; i <= m; i++) { /* set the border position of the first character of the pattern to all indices in array shift having shift[i] = 0 */ if(shift[i] == 0) shift[i] = j; /* suffix becomes shorter than bpos[0], use the position of next widest border as value of j */ if (i == j) j = bpos[j]; } } /*Search for a pattern in given text using Boyer Moore algorithm with Good suffix rule */ static void search(char []text, char []pat) { // s is shift of the pattern // with respect to text int s = 0, j; int m = pat.length; int n = text.length; int []bpos = new int[m + 1]; int []shift = new int[m + 1]; //initialize all occurrence of shift to 0 for(int i = 0; i < m + 1; i++) shift[i] = 0; //do preprocessing preprocess_strong_suffix(shift, bpos, pat, m); preprocess_case2(shift, bpos, pat, m); while(s <= n - m) { j = m - 1; /* Keep reducing index j of pattern while characters of pattern and text are matching at this shift s*/ while(j >= 0 && pat[j] == text[s+j]) j--; /* If the pattern is present at the current shift, then index j will become -1 after the above loop */ if (j < 0) { System.out.printf("pattern occurs at shift = %d\n", s); s += shift[0]; } else /*pat[i] != pat[s+j] so shift the pattern shift[j+1] times */ s += shift[j + 1]; } } // Driver Code public static void main(String[] args) { char []text = "ABAAAABAACD".toCharArray(); char []pat = "ABA".toCharArray(); search(text, pat); } }
Output:
pattern occurs at shift = 0 pattern occurs at shift = 5
Time Complexity of Boyer-Moore Algorithm
The time taken by the Boyer-Moore Algorithm during pattern matching in the worst case is O(m*n). Here, m is the length of the pattern and n is the length of the string provided.
Comparison of the Boyer-Moore Algorithm with other alternatives
| Algorithm | Preprocessing Time | Matching Time |
| Naive Approach | O | (O (n - m + 1)m) |
| Rabin-Karp | O(m) | (O (n - m + 1)m) |
| Finite Automata | O(m|∑|) | O (n) |
| Knuth-Morris-Pratt | O(m) | O (n) |
| Boyer-Moore | O(|∑|) | (O ((n - m + 1) + |∑|)) |
Applications of the Boyer-Moore Algorithm
- This algorithm is quite efficient when a large number of characters are present both in the string as well as in the pattern provided.
- Used in Network Intrusion Detection Systems to find malicious patterns for cyber safety.
You should also learn about Aho-Corasick algorithm for pattern searching as well.
Conclusion
So, in today's blog, we discussed the Boyer-Moore Algorithm and where it can be implemented. We also understood its working via the two strategies along with its comparison with other popular alternatives. At FavTutor, we bring to you the most complex topics in the easiest form.








