In this article, we will learn how to do deletion in a Binary Tree. Before we start off with the topic, let's start with the fundamentals and understand what a binary search tree is.
What are Binary Trees?
Binary search trees (BSTs) are a fundamental data structure used to efficiently store and retrieve data items in sorted order. They are built on the principles of binary trees, where each node can have at most two children, namely the left child and the right child.
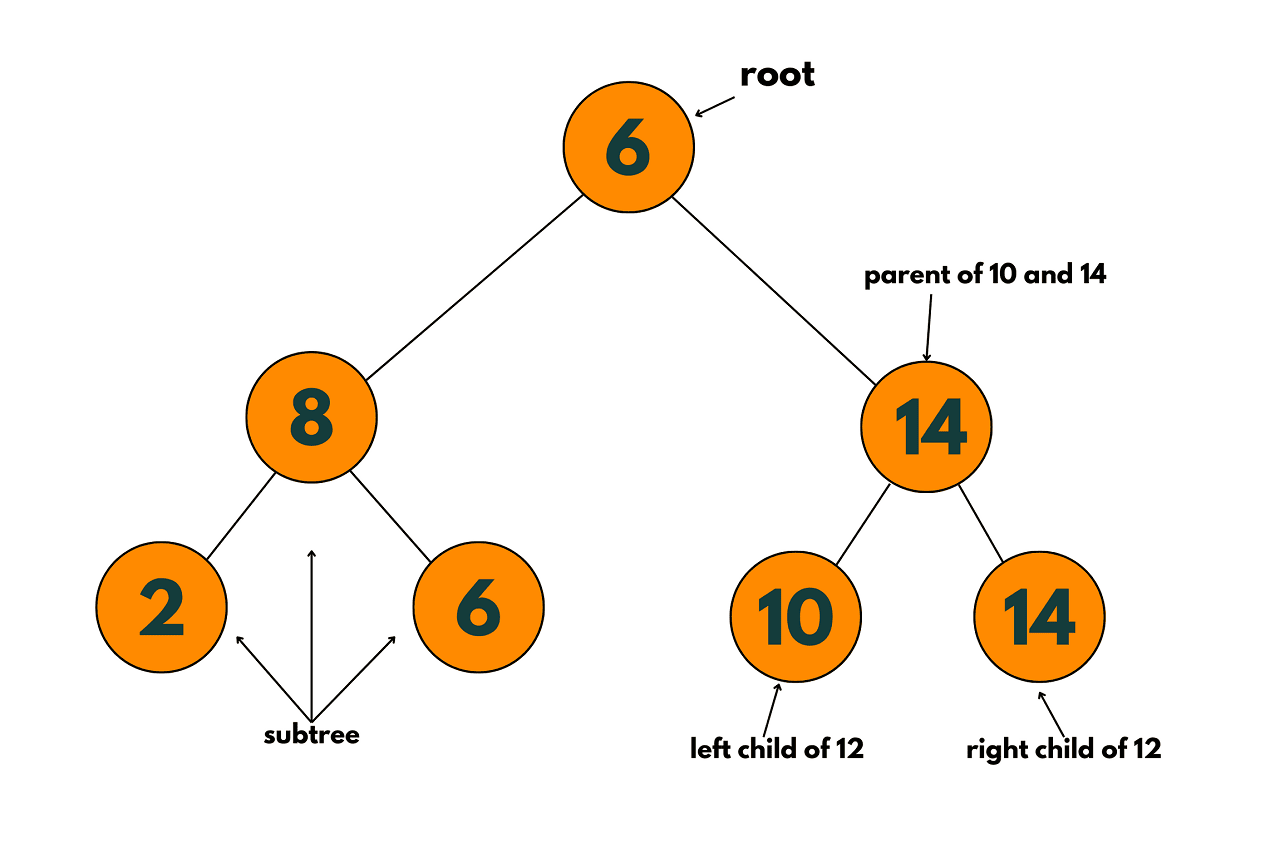
In a BST, each node contains a key, which is the value used to sort the elements in the tree. The left subtree of a node contains keys that are less than the node's key, while the right subtree contains keys that are greater than the node's key. This ordering property allows for efficient searching, insertion, and deletion operations in the tree.
Searching in a BST involves starting at the root node and comparing the search key with the node's key. If the search key is less than the node's key, the search continues in the left subtree. If the search key is greater than the node's key, the search continues in the right subtree.
This process continues until the search key is found or the search reaches a leaf node, indicating that the key is not in the tree. The time complexity of searching in a BST is O(log n) in the average case, where n is the number of nodes in the tree.
Deletion in a Binary Search Tree
Deletion in a binary search tree can be complex because it involves maintaining the balance of the tree while removing a node. When a node is deleted, the binary search property of the tree must be preserved, i.e. that the left subtree of the deleted node must contain only values less than the deleted node, and the right subtree must contain only values greater than the deleted node.
Deletion in a binary search tree can be divided into three cases:
-
The node to be deleted is a leaf node: If the node to be deleted is a leaf node, it can simply be removed from the tree. The parent node of the deleted node must have its corresponding child pointer set to NULL to reflect the change in the tree.
-
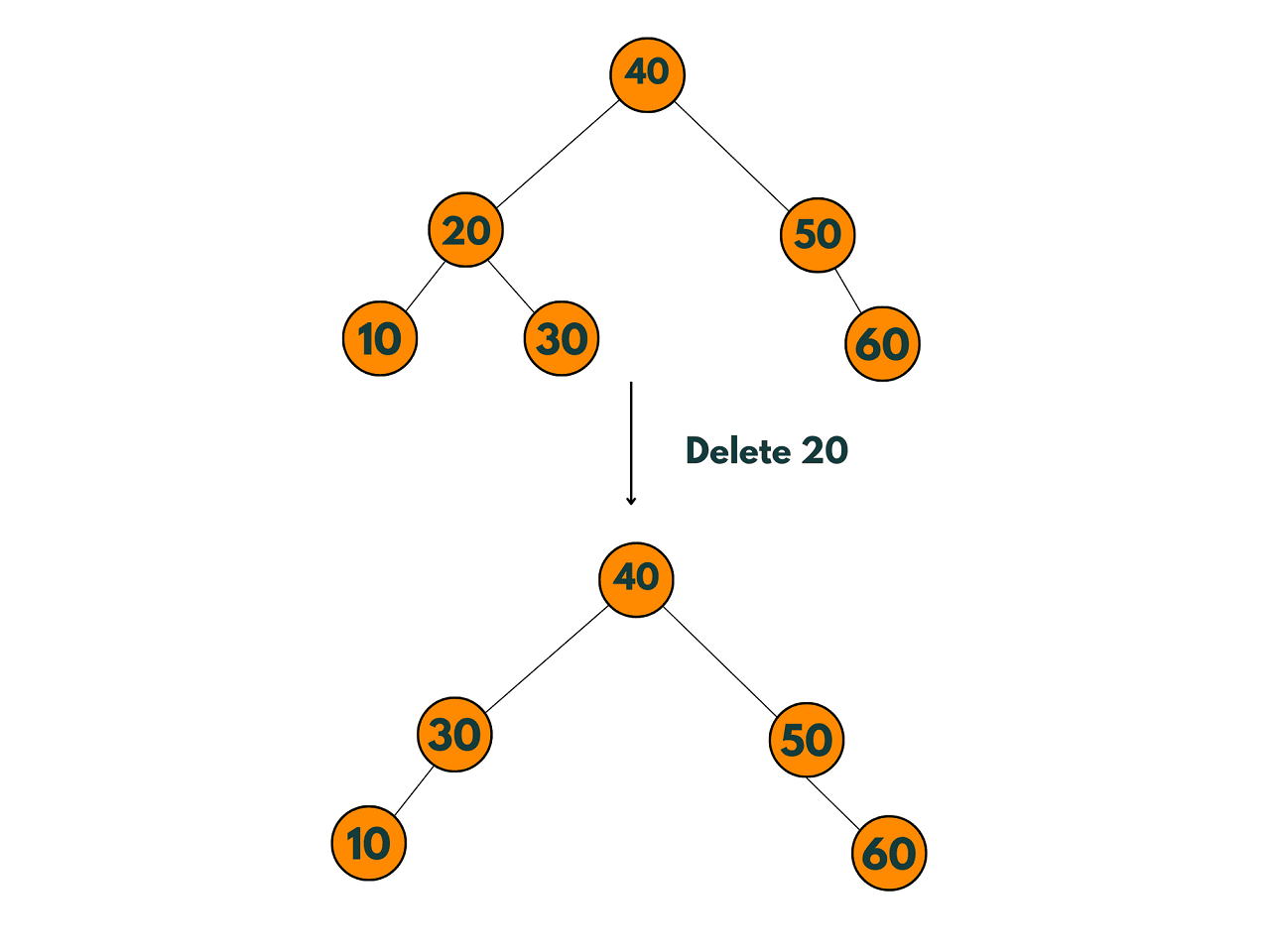
The node to be deleted has only one child: If the node to be deleted has only one child, the child can be promoted to replace the deleted node. The parent node of the deleted node must have its corresponding child pointer updated to point to the promoted child.
-
The node to be deleted has two children: If the node to be deleted has two children, the replacement node can be found by either selecting the minimum value from the right subtree or the maximum value from the left subtree of the node to be deleted. After finding the replacement node, it can be promoted to replace the deleted node. The left subtree of the replacement node (if it exists) must be attached to the left child of the promoted node, and the right subtree of the replacement node (if it exists) must be attached to the right child of the promoted node. The parent node of the deleted node must have its corresponding child pointer updated to point to the promoted node.
If the node to be deleted is a leaf node or a node with only one child, the deletion operation is relatively straightforward. However, if the node to be deleted has two children, finding a replacement node to maintain the binary search property becomes more complicated.
One approach to finding the replacement node is to select the minimum value from the right subtree of the node to be deleted or the maximum value from the left subtree. However, this can be a time-consuming process in larger trees, and there is no guarantee that the replacement node will maintain the balance of the tree.
Another challenge in deletion is maintaining the balance of the tree after the node is deleted. If the tree becomes unbalanced, search operations can become inefficient, defeating the purpose of using a binary search tree.
To address this issue, there are several balancing techniques, such as AVL trees and Red-black trees, that can be used to ensure that the tree remains balanced after a deletion operation.
Deletion in a Binary Search Tree Example
Here are the 4 steps that should be followed:
1) The node to be deleted is a leaf node:
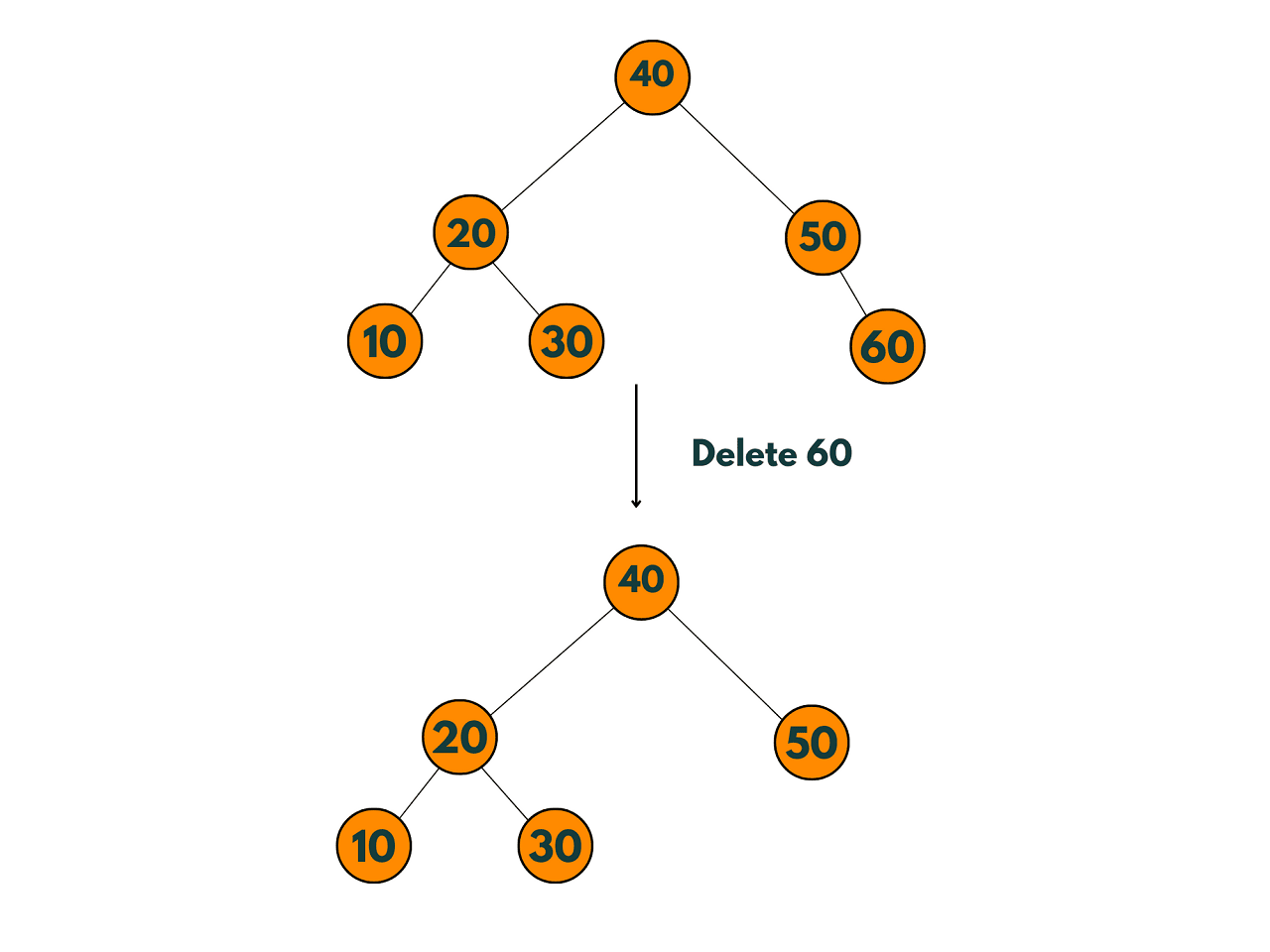
2) The node to be deleted has only one child:
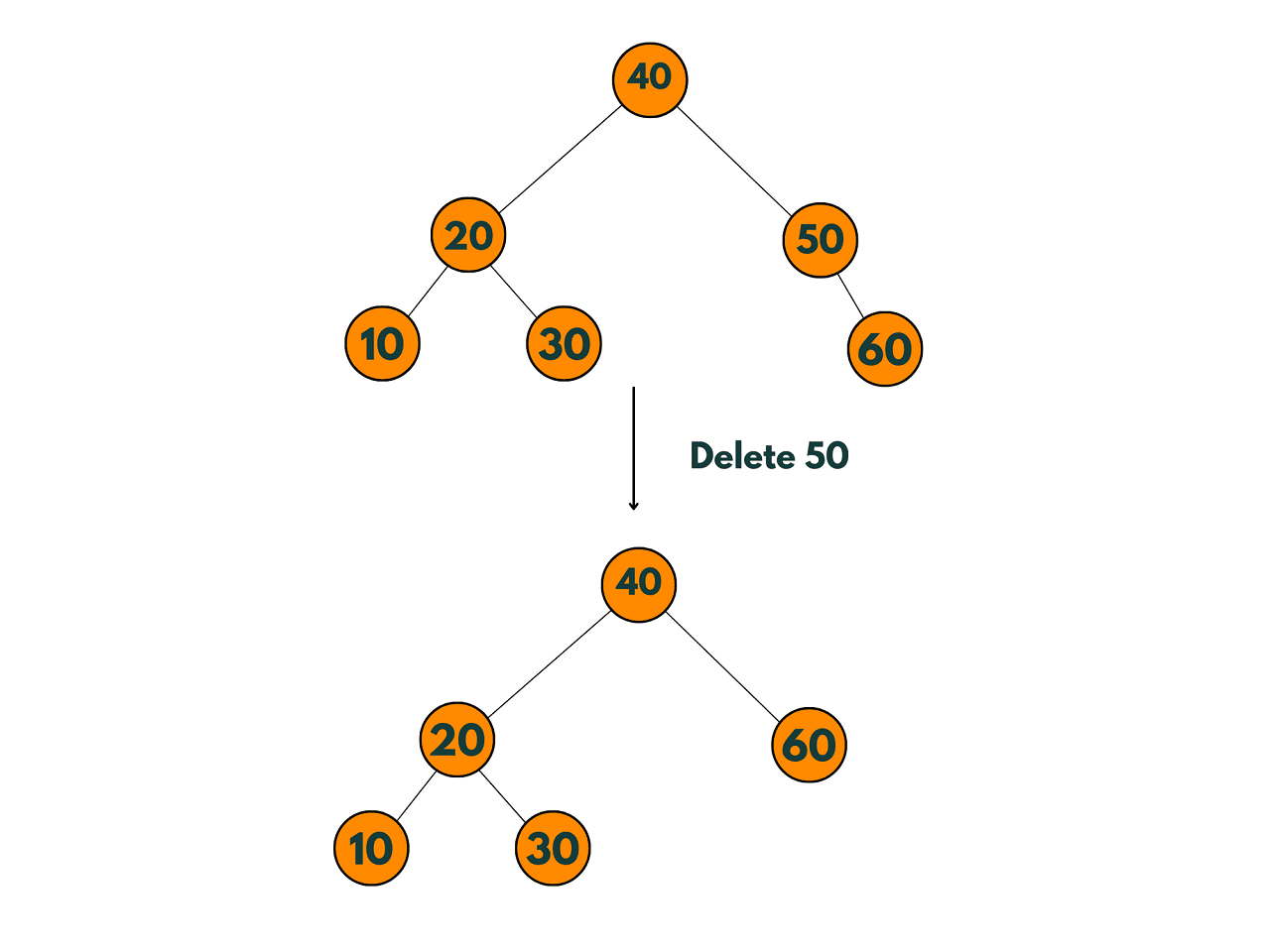
3) The node to be deleted has two children:
Algorithm for Deletion in a Binary Search Tree
Let's take a look at the algorithm for deletion in a binary search tree:
- Start at the root of the binary search tree.
- If the root is NULL, return NULL.
- If the value to be deleted is less than the root's data, recursively call the delete function on the left subtree.
- If the value to be deleted is greater than the root's data, recursively call the delete function on the right subtree.
- If the value to be deleted is equal to the root's data, check if the node to be deleted has one child or no child.
- If the node has only one child or no child, free the memory allocated to the node and return the appropriate child (if it exists).
- If the node to be deleted has two children, find the minimum value in the right subtree (i.e., the leftmost node in the right subtree). Copy the data in the minimum node to the node to be deleted, and recursively call the delete function on the right subtree to delete the minimum node.
- Return the root of the updated binary search tree.
Here is the pseudocode for deletion in a binary search tree:
function deleteNode(root, value):
if root is NULL:
return root
if value < root->data:
root->left = deleteNode(root->left, value)
else if value > root->data:
root->right = deleteNode(root->right, value)
else:
// Case 1: Node to be deleted has only one child or no child
if root->left is NULL:
temp = root->right
free(root)
return temp
else if root->right is NULL:
temp = root->left
free(root)
return temp
// Case 2: Node to be deleted has two children
temp = findMinNode(root->right)
root->data = temp->data
root->right = deleteNode(root->right, temp->data)
return root
C++ Implementation
We will Implement a lazy deletion technique using C++ for deletion in a binary search tree. In this technique, instead of deleting a node from the tree, we mark it as "deleted" and set a flag. The deleted node is then ignored during search and traversal operations.
This can be useful in cases where we expect to delete and insert a lot of nodes in the tree, as it reduces the cost of modifying the tree structure.
Here is an example of an optimized C++ implementation using lazy deletion and recursion:
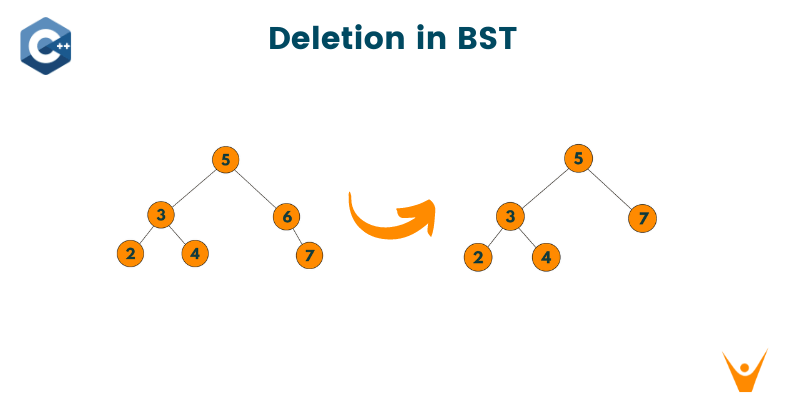
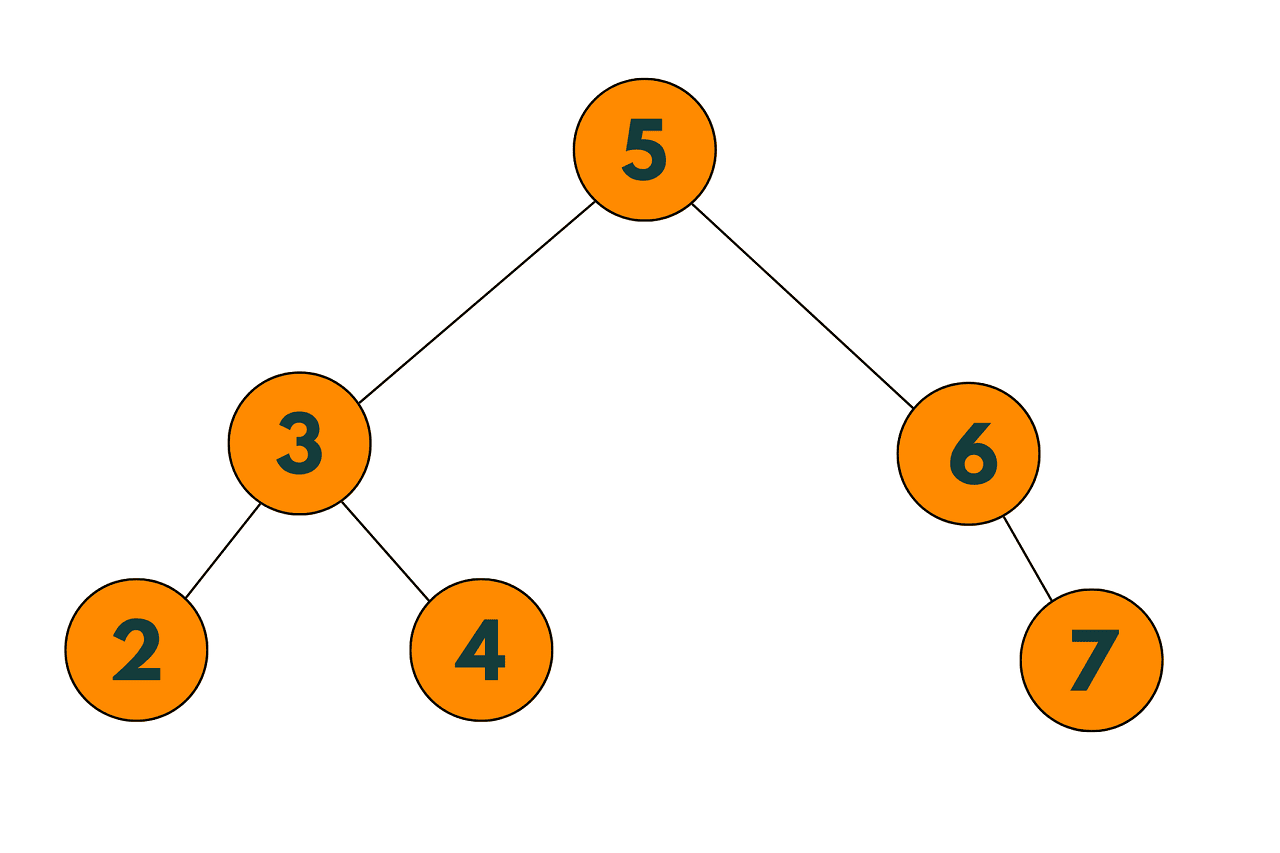
#include struct TreeNode { int val; TreeNode* left; TreeNode* right; bool deleted; // added for lazy deletion TreeNode(int x) : val(x), left(nullptr), right(nullptr), deleted(false) {} }; TreeNode* deleteNode(TreeNode* root, int key) { if (!root) return nullptr; if (key < root->val) { root->left = deleteNode(root->left, key); } else if (key > root->val) { root->right = deleteNode(root->right, key); } else { // node to be deleted found root->deleted = true; // mark as deleted instead of deleting node // check if both children exist if (root->left && root->right) { // find the successor (smallest node in the right subtree) TreeNode* successor = root->right; while (successor->left) { successor = successor->left; } // copy the value of the successor to the current node root->val = successor->val; // mark the successor as deleted instead of deleting node successor->deleted = true; // recursively delete the marked node root->right = deleteNode(root->right, successor->val); } else { // if only one child or no child, return the other child TreeNode* child = root->left ? root->left : root->right; return child; } } return root; } void inorderTraversal(TreeNode* root) { if (root) { inorderTraversal(root->left); if (!root->deleted) { std::cout << root->val << " "; } inorderTraversal(root->right); } } int main() { TreeNode* root = new TreeNode(5); root->left = new TreeNode(3); root->right = new TreeNode(6); root->left->left = new TreeNode(2); root->left->right = new TreeNode(4); root->right->right = new TreeNode(7); std::cout << "Before deletion: "; inorderTraversal(root); std::cout << std::endl; root = deleteNode(root, 6); std::cout << "After deletion: "; inorderTraversal(root); std::cout << std::endl; return 0; }
Output:
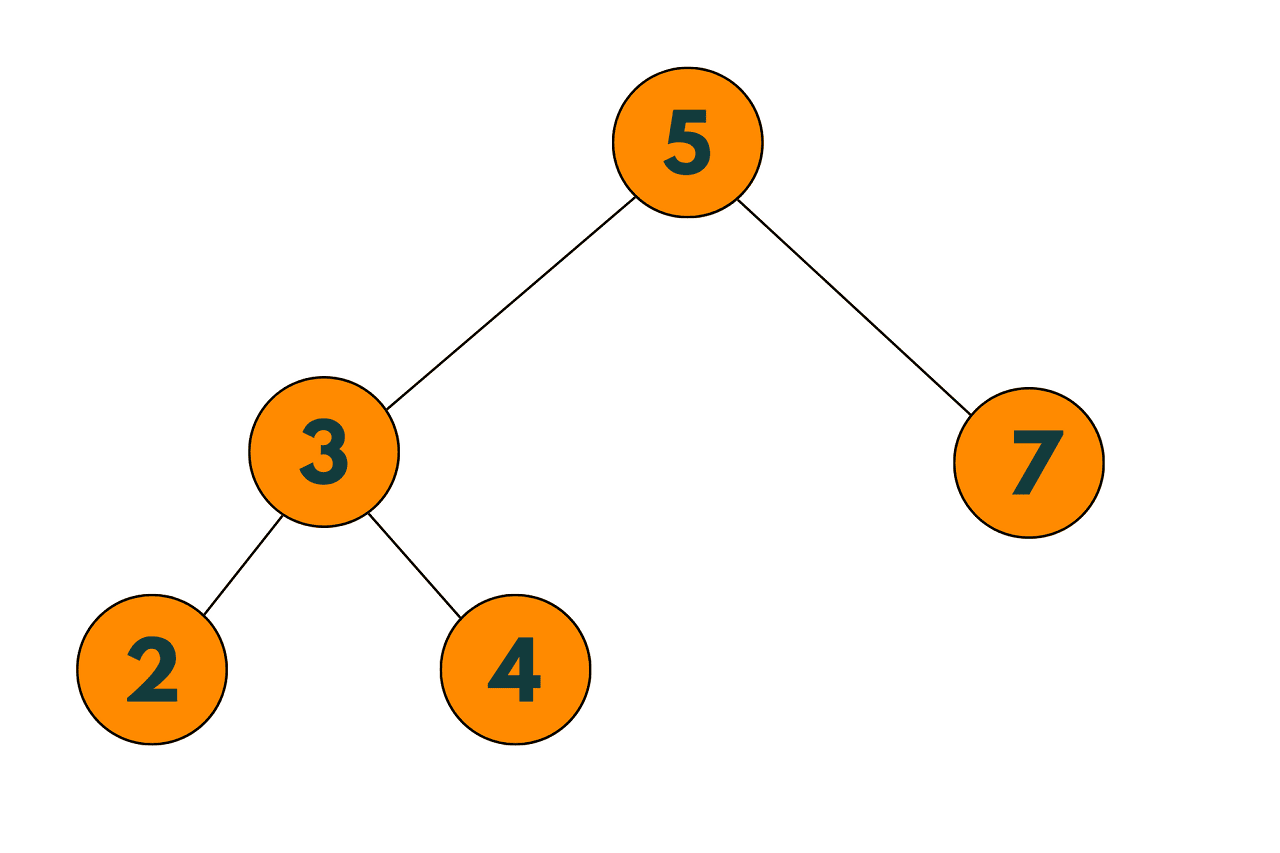
Before deletion: 2 3 4 5 6 7 After deletion: 2 3 4 5 7
ORIGINAL TREE:
TREE AFTER DELETION:
In this implementation, the TreeNode struct has an additional boolean field called 'deleted' to keep track of nodes that have been marked as deleted. The deleteNode function marks the node to be deleted as deleted and returns the root of the updated tree.
The inorderTraversal function performs an in-order traversal of the tree, skipping over any nodes that have been marked as deleted.
Time & Space Complexity
The time complexity of deletion in a binary search tree using lazy deletion and recursion is O(h), where h is the height of the tree.
The worst-case scenario is when the tree is completely unbalanced, where the height of the tree is equal to the number of nodes in the tree. In this case, the time complexity of deletion is O(n), where n is the number of nodes in the tree.
However, in a balanced binary search tree, the height of the tree is O(log n), where n is the number of nodes in the tree. In this case, the time complexity of deletion is O(log n).
Conclusion
In conclusion, binary search trees are an essential data structure used to efficiently store and retrieve data items in sorted order. The use of lazy deletion does not change the time complexity of deletion, as the algorithm still traverses the tree recursively in the same way.