Implementing DFS in Java | Depth First Search Algorithm

Graph traversals are some of the more subtle topics to learn before one can take a deep dive into the more complex algorithmic problems related to graphs. In this article, we will be having an in-depth look at DFS Algorithm and how to implement Depth-First Search in Java.

What is Depth First Search?

Graph traversal is the process by which one can travel from one node (called the source) to all other nodes of the graph. The order of nodes traced out during the process of traversal depends on the algorithm used. Graph traversal is of two main types: Breadth-first Search and depth-first Search.

Depth First Search (DFS) is an algorithm of graph traversal that starts exploring from a source node (generally the root node) and then explores as many nodes as possible before backtracking. Unlike breadth-first search, the exploration of nodes is very non-uniform by nature.

DFS Algorithm

The general process of exploring a graph using depth-first search includes the following steps:

• Take the input for the adjacency matrix or adjacency list for the graph.
• Initialize a stack.
• Push the root node (in other words, put the root node at the beginning of the stack).
• If the root node has no neighbors, stop here. Else push the leftmost neighboring node which hasn’t already been explored into the stack. Continue this process till a node is encountered that has no neighbors (or whose neighbors have all been added to the stack already) – stop the process, pop the head, and then continue the process for the node that is popped.
• Keep repeating this process till the stack becomes empty.

(If you aren’t familiar with push and pop operations – push adds an element to the top of the stack, while pop removes an element from the top of the stack).

DFS Algorithm Example

Let’s work with a small example to get started. We are using the graph drawn below, starting with 0 as the root node.

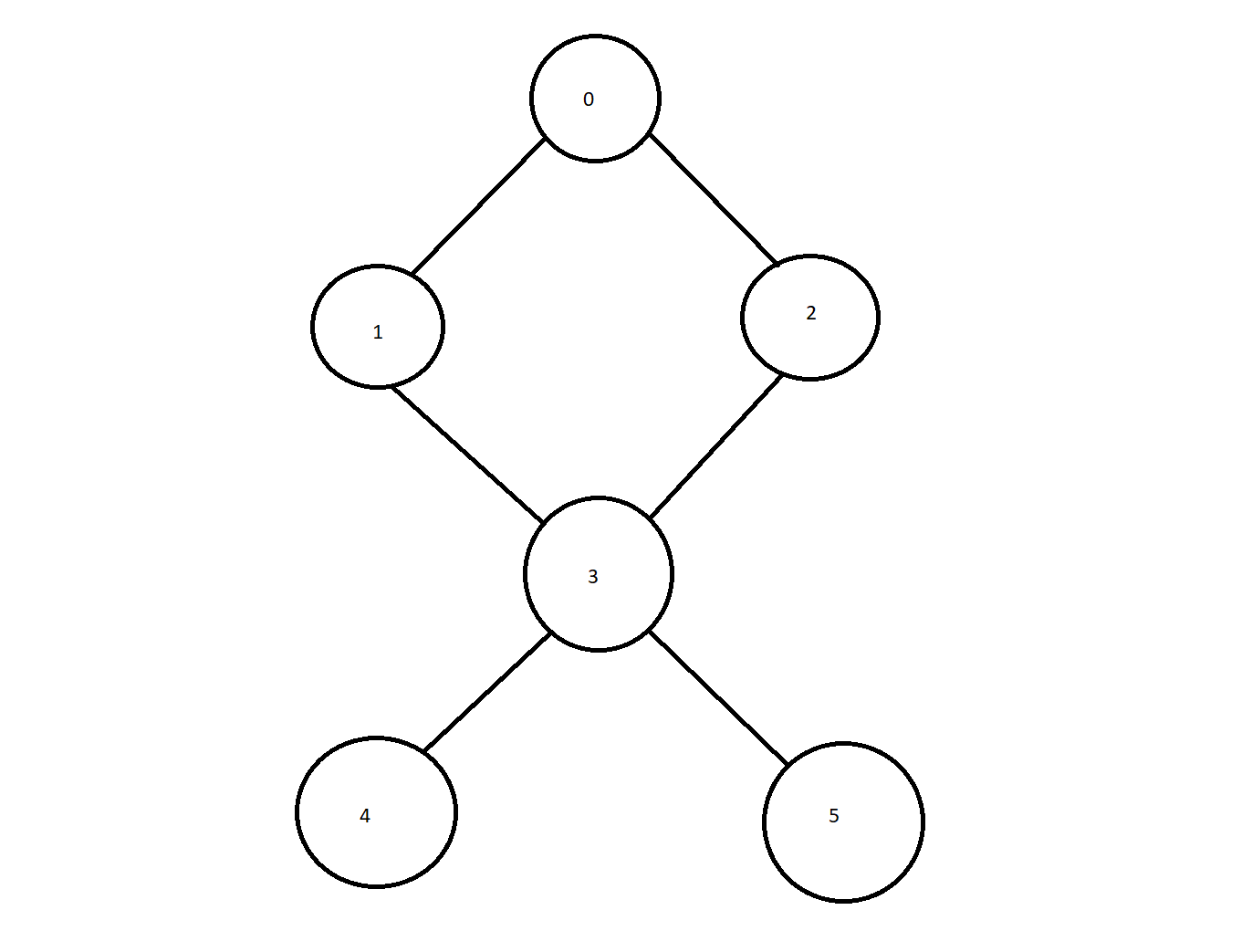
Iteration 1: Push(0).

Stack after iteration 1 :

Iteration 2: Push(1).

Stack after iteration 2 :

Iteration 3: Push(3).

Stack after iteration 3 :

Iteration 4: Push(4).

Stack after iteration 4 :

Iteration 5: Pop(4).

Stack after iteration 5 :

Iteration 6: Push(5).

Stack after iteration 6 :

Iteration 7: Pop(5).

Stack after iteration 7 :

Iteration 8: Push(2).

Stack after iteration 8 :

Iteration 9: Pop(2).

Stack after iteration 9 :

Iteration 10: Pop(3).

Stack after iteration 10 :

Iteration 11: Pop(1).

Stack after iteration 11 :

Iteration 12: Pop(0).

Stack after iteration 11 :

One thing that should be pretty noticeable is that DFS runs comparatively longer than that of an equivalent BFS structure for the same graph. Since the stack is again empty at this point, we will stop the process.

Edge Cases

Now, there’s always the risk that the graph being explored has one or more cycles. This means that there’s a chance of getting back to a node that we have already explored.

How do we determine if a node has been explored or not? It’s simple – we simply maintain an array for all the nodes. The array at the beginning of the process will have all of its elements initialized to 0 (or false).

Once a node is explored, the corresponding element in the array will be set to 1 (or true). We simply push nodes to the stack if the value of their corresponding element in the array is 0 (or false). There’s still another problem to solve.

What happens if the graph given is a disconnected graph (meaning that it has multiple connected components instead of a single component)? This would mean that the results obtained would be skewed because all nodes would never be explored. The solution is to iterate through the unexplored nodes and manually use the DFS algorithm to explore each component individually.

Of course, this means that one would need to take the help of an array to mark the nodes that have already been explored up to a certain point.

Applications of Depth-First Search Algorithm

Depth First Search has a lot of utility in the real world because of the flexibility of the algorithm. These include:

• All traversal methods can be used for the detection of cycles in graphs. Cycle detection is done using DFS by checking for back edges.
• Both DFS and BFS can be used for producing the minimum spanning tree and for finding the shortest paths between all pairs of nodes (or vertices) of the graph.
• DFS can be used for topological sorting of a graph. In topological sorting, the nodes of the graph are arranged in the order in which they appear on the edges of the graph.
• DFS can be used to check if a graph is bipartite or not. A bipartite graph is such that all nodes in the graph can be divided into two sets such that the edges of the graph connect one vertex from each set.
• DFS can be used for finding the strongly connected components of a graph. Strongly connected components are such that all of the nodes in the component are connected to one another.

Implementing DFS in Java

There are multiple ways to implement DFS in Java. We will be using an adjacency list for the representation of the graph and will be covering both recursive as well as and iterative approaches for the implementation of the algorithm. The graph used for the demonstration of the code will be the same as the one used for the above example.

Recursive implementation

The recursive implementation for the DFS algorithm in Java is as follows:

import java.io.*;
import java.util.*;
 

class Graph {
    private int V;                              //number of nodes
 
    private LinkedList<Integer> adj[];              //adjacency list
 
    public Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
{
          adj[i] = new LinkedList();
    	}
 
    void addEdge(int v, int w)
    {
        adj[v].add(w);                              //adding an edge to the adjacency list (edges are bidirectional in this example)
    }
 

    void DFSUtil(int vertex, boolean nodes[])
    {

        nodes[vertex] = true;                         //mark the node as explored
        System.out.print(vertex + " ");
        int a = 0;
 
        for (int i = 0; i < adj[vertex].size(); i++)  //iterate through the linked list and then propagate to the next few nodes
            {
                a = adj[vertex].get(i);
                if (!nodes[a])                    //only propagate to next nodes which haven't been explored
                {
                    DFSUtil(a, nodes);
                }
            }  
    }

    void DFS(int v)
    {
        boolean already[] = new boolean[V];             //initialize a new boolean array to store the details of explored nodes
        DFSUtil(v, already);
    }
 
    public static void main(String args[])
    {
        Graph g = new Graph(6);
 
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 0);
        g.addEdge(1, 3);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 4);
        g.addEdge(3, 5);
        g.addEdge(4, 3);
        g.addEdge(5, 3);
 
        System.out.println(
            "Following is Depth First Traversal: ");
 
        g.DFS(0);
    }
}

Iterative implementation

The iterative implementation of DFS in Java follows:

import java.util.*; 
  

 class Graph 
    { 
        int V;                                          //number of nodes
          
        LinkedList<Integer>[] adj;                      //adjacency list
          
        Graph(int V) 
        { 
            this.V = V; 
            adj = new LinkedList[V]; 
              
            for (int i = 0; i < adj.length; i++) 
                adj[i] = new LinkedList<Integer>(); 
              
        } 
          
        void addEdge(int v, int w) 
        { 
            adj[v].add(w);                              //adding an edge to the adjacency list (edges are bidirectional in this example)
        } 
          
        void DFS(int n) 
        { 
            boolean nodes[] = new boolean[V]; 
      
            Stack<Integer> stack = new Stack<>(); 
              
            stack.push(n);                                    //push root node to the stack
            int a = 0;
              
            while(!stack.empty()) 
            { 
                n = stack.peek();                       //extract the top element of the stack
                stack.pop();                            //remove the top element from the stack
                  
                if(nodes[n] == false) 
                { 
                    System.out.print(n + " "); 
                    nodes[n] = true; 
                } 
                  
                for (int i = 0; i < adj[n].size(); i++)  //iterate through the linked list and then propagate to the next few nodes
            {
                a = adj[n].get(i);
                if (!nodes[a])                    //only push those nodes to the stack which aren't in it already
                {
                    stack.push(a);                          //push the top element to the stack
                }
            }  
                  
            } 
        } 
      
    public static void main(String[] args)  
    { 
        Graph g = new Graph(6); 
          
        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 0);
        g.addEdge(1, 3);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 4);
        g.addEdge(3, 5);
        g.addEdge(4, 3);
        g.addEdge(5, 3); 
              
        System.out.println("Following is the Depth First Traversal"); 
        g.DFS(0); 
    } 
} 

Output:

Following is Depth First Traversal:

0 1 3 4 5 2

Time and Space Complexity

The running time complexity of the DFS algorithm in Java is O(V+E) where V is the number of nodes in the graph, and E is the number of edges.

Since the algorithm requires a stack for storing the nodes that need to be traversed at any point in time, the space complexity is the maximum size of the stack at any point of time. Since this can extend to V slots for a linear graph, the maximum space complexity is O(V).

Why DFS is Faster than BFS?

DFS appears faster than BFS in certain situations due to its ability to explore deep branches in a graph more quickly. This advantage can be seen when the target is located relatively deep in the data structure. DFS prioritizes depth, traversing as far down as possible before backtracking.

Is DFS a Recursion or Stack?

We implement DFS using a stack or recursion. A function can call itself using the sophisticated programming concept of recursion. By invoking the DFS function on each subsequent node, recursion is employed in the context of DFS to traverse all the nodes in a graph. As a result, the code is clearer and simpler to comprehend.

On the other hand, a stack can also be used to implement DFS. This method keeps track of the nodes that need to be visited using a stack. Starting at the root node, the algorithm puts data into the stack. The method then pops a node from the stack, visits it, and pushes all of its unvisited adjacent nodes into the stack while it still contains nodes. Until the stack is empty, this process is repeated.

Although the stack-based approach might be more effective in some situations, the recursive approach is generally easier to understand and simpler.

What is the disadvantage of the DFS algorithm?

Although DFS is a strong method, it has a significant drawback: if the graph contains cycles, it may become stuck in an unending loop. This happens when the algorithm revisits a node that is a component of a cycle and has already been visited. The algorithm will keep looping back to the same nodes without ever ending.

DFS often uses a technique to keep track of the visited nodes in order to prevent this issue. This prevents infinite loops and prevents the algorithm from visiting the same node more than once. This method, however, increases the algorithm's overhead and could make it slower.

BFS, on the other hand, is not affected by this drawback because it visits every node at the exact same depth level before going to the next level.

Conclusion

DFS algorithm is one of the most important algorithms to master if one wants to solve problems with graphs. One quick look through our implementation of the depth-first search in Java should be enough to get your basics of the algorithm ready.