We are back with yet another competitive coding problem. Till now you must be aware of how important these problems are to get your dream job, as most companies like to assess their problem-solving skills. In this article, we are going to discuss a problem called “Find peak element” with different approaches.
Find Peak Element Problem
Before jumping straight to the approach, we must know what the problem is. Here is the problem statement: "The problem states that we are given an array of numbers and we are required to find a peak element from it."
Now, what is a peak element? A peak element is that number in the given array which is greater than its neighboring elements. And for an end element to be the peak element it just needs to be greater than the element before or after it.
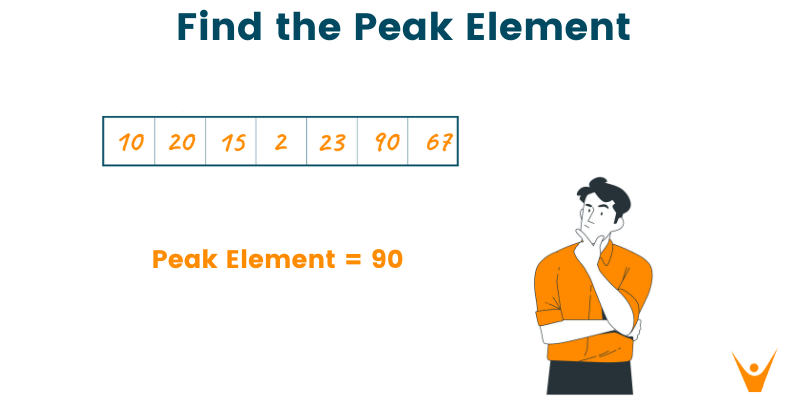
Let us take an example to illustrate this better. Suppose we are given the array arr that contains values as follows: Arr= {10, 20, 15, 2, 23, 90, 67}.
In this array, the peak element can be either 20 or 90. Why? because the neighbors of both the elements (10, 15 in case of 20 and 23, 67 in case of 90) are smaller than the element itself.
In some special cases, like if the array is sorted in ascending order. Then, the last element of the array is the peak element. However, if the array is sorted in descending order then the first element is the peak element.
Naive Approach
The first solution that might come into your mind is that we can traverse through the array from the second element to the second last element. And for each element, we can check the element before and after it. And if both the elements are smaller than the current element then congratulations, we have our peak element.
But before traversing the whole array we need to rule out the possibility of the first and last element being the peak element. To do this, we need to check the value of the second element and if this value is greater than the first element then the first element is the peak element. The same is done for the last element except for the second element we check the value of the second last element.
Now, this approach works very well and achieves the task we are aiming for. But it has a time complexity of O(n), since all the elements need to be traversed once in the worst case, and we have a more efficient approach available to solve this.
Using Modified Binary Search
We employ a modified concept of binary search to solve this problem more efficiently. We suggest you go through the binary search article before continuing. However, if you are already familiar with it then you can continue.
In this approach, we check the value of the middle element with its neighboring elements. If it is greater then we have found the peak element and returned it. If this is not the case, then we check the value of the element left to the middle value. If the left value is greater than the middle value then the peak element must be present on the left side. This algorithm is then called recursively on the left side.
However, if the left element is smaller then the right element is checked. If the value of the right element is greater than the middle element then the algorithm is recursively called on the left side of the array. This process is continued until we find a peak element or the lower bound is smaller than the upper bound.
Let us now discuss the algorithm of this approach:
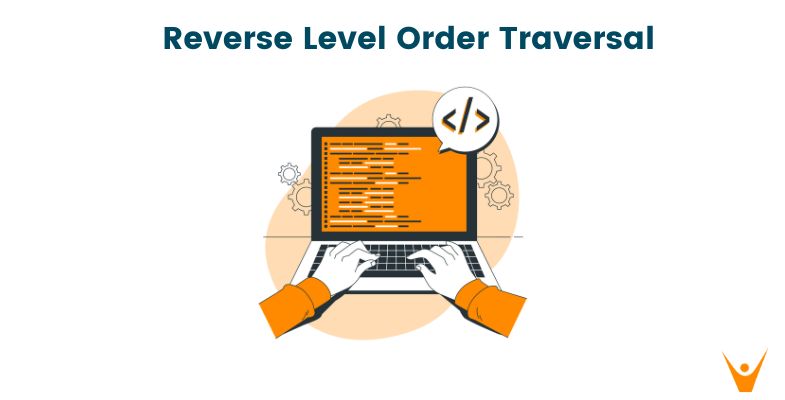
- Create two variables, LowerBound and UpperBound, and set them to 0 and n-1, respectively.
- Iterate the steps below until the lower bound is less than the upperbound and LowerBound = UpperBound.
- Check whether the mid-value or index mid = (LowerBound+UpperBound)/2, is the peak element; if it is, print the element and exit the loop.
- Otherwise, if the element on the right side of the middle element is larger, look for the peak element on the right side, i.e. update LowerBound = mid + 1.
- Otherwise, if the element on the left side of the middle element is greater, look for the peak element on the left, i.e. update UpperBound = mid – 1.
How to Find Peak Element in Array?
In the first recursion since the mid element is smaller than its neighboring elements, therefore, it cannot be the peak element. The element of the right to the mid is checked, and since its value is greater than the mid element, that is why we continue to check for the peak element on the right side of the array. The LowerBound variable is made to store the mid+1 index i.e. 4.

In the second recursive call, the element at the mid index is 90 and since it is greater than both of its neighboring elements, it is returned and we get our answer as 90.
Finding Peak Element using Java
Here is the implementation in Java to find the peak element in an array:
public class findPeakElement { private static int findPeakUtil(int[] arr,int low,int high,int n){ //finding the middle element of array //this method is more reliable int mid=low+(high-low)/2; //Compare middle element with its neighbours if((mid==0 || arr[mid-1]<=arr[mid]) && (mid==n-1 || arr[mid+1]<=arr[mid])) return mid; // If middle element is not peak and its // left neighbour is greater than it, // then left half must have a peak element else if(mid>0 && arr[mid-1]>arr[mid]) return findPeakUtil(arr,low,(mid-1),n); // Similarly,if the middle element is not the peak and // its right side element is greater than it, // then right half must have a peak else return findPeakUtil(arr,(mid+1),high,n); } public static void main(String[] args) { int[] arr={10,20,15,2,23,90,67}; int n=arr.length; System.out.println("The peak point is "+arr[findPeakUtil(arr,0,n-1,n)]); } }
Finding Peak Element using Python
Here is the Python code to solve the 'Find Peak Element' problem using binary search:
def findPeakUtil(arr, lowerBound, upperBound, n): # Find the middle index mid = lowerBound + (upperBound - lowerBound)/2 mid = int(mid) # Compare middle element with its # neighbours if ((mid == 0 or arr[mid - 1] <= arr[mid]) and (mid == n - 1 or arr[mid + 1] <= arr[mid])): return mid elif (mid > 0 and arr[mid + 1] > arr[mid]): return findPeakUtil(arr, (mid + 1), upperBound, n) else: return findPeakUtil(arr, lowerBound, (mid - 1), n) arr = [10, 20, 15, 2, 23, 90, 67] n = len(arr) print("The peak point is", arr[findPeakUtil(arr, 0, n - 1, n)])
Output:
The peak point is 90
This approach has a time complexity of O( log n) because at each step the size of the array becomes half. You can also compare it with the binary search technique to understand it better. Since this algorithm employs no extra space, therefore, its space complexity is O(1).
Finding Peak Element using C++
Here is the C++ Program to find the peak element in an array:
#include <iostream> using namespace std; int findPeak(int arr[], int n) { if (n == 1) // array of size 1 is always a peak return arr[0]; if (arr[0] >= arr[1]) // first element is a peak return arr[0]; if (arr[n-1] >= arr[n-2]) // last element is a peak return arr[n-1]; for (int i = 1; i < n-1; i++) { // check for peak element in the middle if (arr[i] >= arr[i-1] && arr[i] >= arr[i+1]) return arr[i]; } return -1; // no peak element found } int main() { int arr[] = { 1, 3, 20, 4, 1, 0 }; int n = sizeof(arr) / sizeof(arr[0]); int peak = findPeak(arr, n); if (peak == -1) cout << "No peak element found"; else cout << "Peak element is " << peak; return 0; }
The findPeak function in the code above requires an input array as well as its size as inputs. The function first determines if the array is of size 1, and if it is, it returns the array's single peak element.
The function determines whether or not the first element of an array with a size larger than one is a peak element. If so, it is then given back. It also determines whether the final element is a peak element. If so, it is then given back.
Using Iterative Binary Search
The problem can be resolved using the binary search method in O(log n) time complexity. This is how the algorithm operates:
- Determine the array's middle element.
- Verify the peak element status of the middle element.
- Check to see if the middle element's left neighbor is greater than the middle element if the middle element is not a peak element. If it is, look for a peak element on the array's left side. If not, look on the right side of the array for a peak element.
Until we locate a peak element, the method described above is repeated.
Here is the C++ code for an iterative binary search method to locate a peak element:
#include <iostream> using namespace std; int findPeak(int arr[], int n) { int low = 0, high = n - 1; while (low <= high) { int mid = (low + high) / 2; if ((mid == 0 || arr[mid - 1] <= arr[mid]) && (mid == n - 1 || arr[mid + 1] <= arr[mid])) return arr[mid]; else if (mid > 0 && arr[mid - 1] > arr[mid]) high = mid - 1; else low = mid + 1; } return -1; } int main() { int arr[] = { 1, 3, 20, 4, 1, 0 }; int n = sizeof(arr) / sizeof(arr[0]); int peak = findPeak(arr, n); if (peak == -1) cout << "No peak element found"; else cout << "Peak element is " << peak; return 0; }
An input array plus its size is first provided to the function. The peak element in the array can be located using the findPeak function. The input array as well as its size are the two arguments required by the function. Two pointers, low and high, that point to the starting and last members of the array, respectively, are initialized as the function begins.
The peak element is looked for using a while loop. The formula (low + high) / 2 is used to determine the center member of the array during each iteration of the loop. Next, it is determined whether or not the middle element is a peak element. It is returned if it is a peak element.
Otherwise, the peak element must be within the left half of the array, because the high pointer is changed to mid-1 if the middle element's left neighbor is greater above the middle element.
Conclusion
In this article, we discussed how to find the peak element in an array with implementation in Java, C++, and Python. While solving such types of problems it is necessary to understand that just solving them is not the key but solving them efficiently is. For more assistance, get our premium programming help online from experts.