Number theory is a very popular study of numbers. There are various types of special numbers that exist in today's world. One of these special numbers is the Happy number.
Sounds interesting? Let's dive into it.
What is a Happy Number?
A happy number is defined as a number that can be replaced by the sum of the squares of its digit repeatedly and after some repetitions, it will yield the number 1.
Too much technical jargon? Let us simplify this. Let us understand this with an example.
An Example
Consider the number 19. The digits in 19 are? 1 and 9, obviously. Now square the digits, and we get 1 and 81, add them, what do we get? We get 82. Now the digits in 82 are 8 and 2, so we square the digits again, and we get 64 and 4. Add them and we get 68.
Now square the digits in 68, that is 6 and 8, and we get 36 and 64. Add them we get 100. The digits in 100 are 1,0 and 0. Square them we get 1, 0, and 0. Adding all the squares we get the number 1.
Did you observe how we repeatedly replace the number with the sum of the square of its digit and after a few repetitions we end up with 1? Therefore 19 is a happy number. You can be happy too, you understand what happy numbers are now.
Intuition behind a Happy Number
As we saw in the previous examples, a happy number is any number that can become one if we keep replacing it with the sum of the square of its digits. But logically speaking, how do we identify if a number is a happy number or not? The most obvious method would be to keep replacing the number with the square of its digits.
But this raises a dilemma for us. How do we know when to stop the recalculation and conclude that the number given to us is not a happy number? Let us try to understand the intuition behind a happy number with the help of another example.
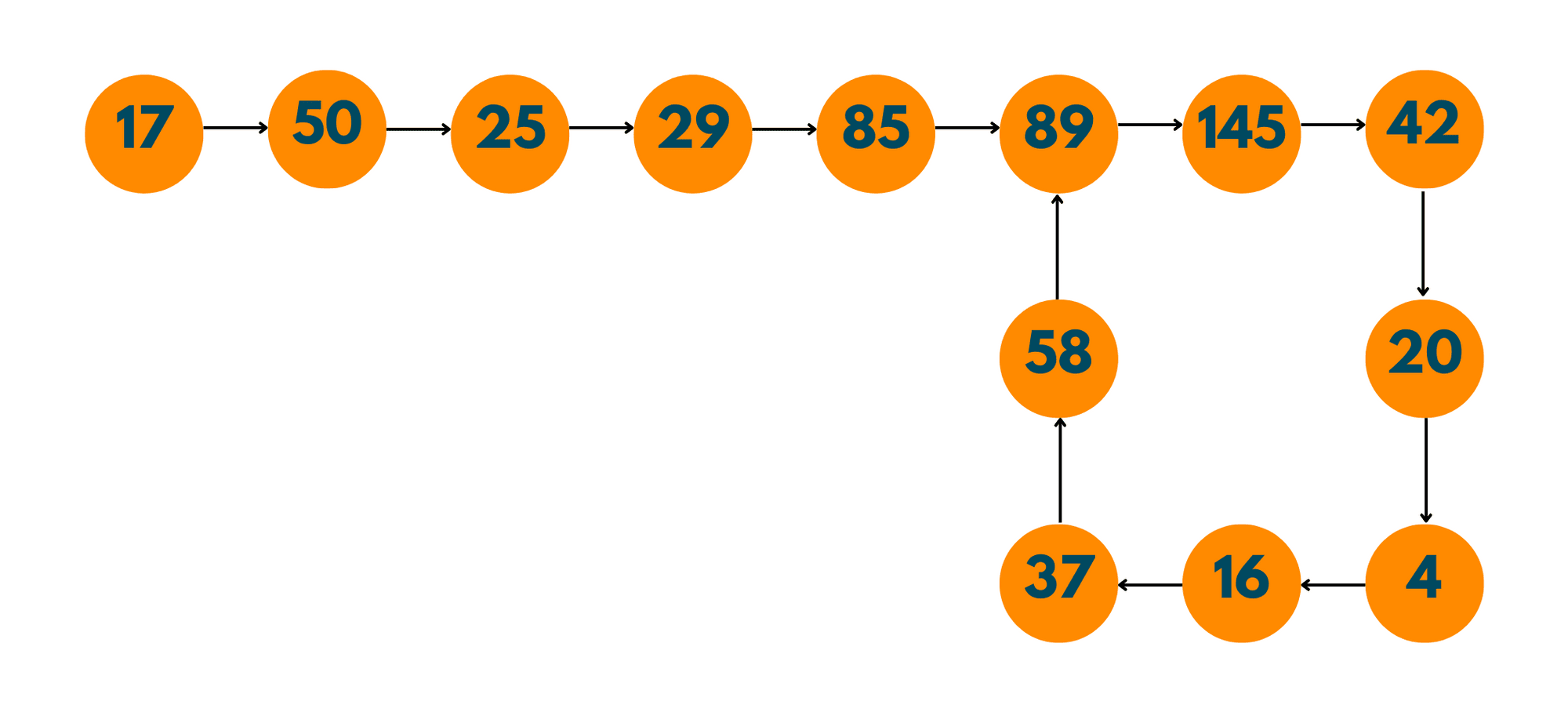
Consider the number 17, and let us perform the calculations on it.
- For 17, the digits are 1 and 7, and the sum of the squares is 50
- For 50, the digits are 5 and 0, and the sum of the squares is 25
- For 25, the digits are 2 and 5, and the sum of the squares is 29
- For 29, the digits are 2 and 9, and the sum of the squares is 85
- For 85, the digits are 8 and 5, and the sum of the squares is 89
- For 89, the digits are 8 and 9, and the sum of the squares is 145
We keep repeating this process until we get to 58 then the digits are 5 and 8 and the sum of the squares is 89, can you guess the next number? The next number will be 145 and then so on until we come back to 58 again.
Do you identify a pattern? If during the repetitions we come across a number that has already occurred once, we can conclude that the number we have received is not a happy number. This is the intuition behind identifying a happy number.
Let us now look at code examples of how to solve such problems.
03 Methods to Solve a Happy Number
There are three different approaches that you can take to solve this problem. We have already learned the intuition behind finding out a happy number.
We need to find the sum of the digits of a number constantly and if we get a one then we can say a number is a happy number, or if we get a number that has already occurred in the sequence we can say it is not a happy number.
01) Naive approach
The approach that you saw earlier in the example is a naive approach. In order to implement it as a code, we will use a set variable that will store all the new numbers that are formed when we keep replacing the given number with the sum of the square of its digits.
Then if we get one, we will say a number is a happy number, or if we get a number that is already present in the set we will say it is not a happy number. Here is the code in Python:
def squaredsum(num): sum = 0 while(num): sum += (num%10) ** 2 num = num//10 return sum def happynumber(num): record = set() while(1): num = squaredsum(num) if num==1: return True if num in record: return False record.add(num) num = int(input("Enter a number: ")) if happynumber(num): print(num," is a happy Number") else: print(num," is not a happy number")
Output:
Enter the number: 19 19 is a happy number
Time Complexity: O(n*log(n))
Space Complexity: O(n)
02) Without using extra space
What do you think is a disadvantage of the previous method? It uses a lot of space since we have to keep a track record of all the new numbers that are created. A better approach uses the concept of linked lists.
In this method, we use two variables, a slow and a fast variable. The slow variable moves one step at a time, whereas the fast variable moves two steps at a time. They are moving towards each other and if both of them end at 1 then the given number is happy, but if both of them end up at any different number then the given number is not happy.
Here is the python code for this method:
def squaredsum(num): sum = 0 while(num): sum += (num%10) ** 2 num = num//10 return sum def happynumber(num): slow = num fast = num while(True): slow = squaredsum(slow) fast = squaredsum(squaredsum(fast)) if (slow!=fast): continue else: break return (slow==1) num = int(input("Enter a number: ")) if happynumber(num): print(num, "Happy Number") else: print("Not a happy number")
Output:
Enter the number: 13 13 is a happy number
Time Complexity: O(n*log(n))
Space Complexity: O(1)
03) Alternative method to not using extra space
For the alternative method, let us discover a new thing about happy numbers. The only one-digit numbers that are happy are 1 and 7, so when we replace a given number with the sum of the square of its digits if we end up with 1 or 7 during the repetition we can conclude that the given number is a happy number.
Here is the code in Python:
def happynumber(num): if num==1 or num==7: return True else: total,n = num, num while total>9: total = 0 while n>0: total += (n%10)**2 n //=10 if total == 1: return True n = total if total == 7: return True return False num = int(input("Enter a number: ")) if happynumber(num): print(num, "Happy Number") else: print("Not a happy number")
Output:
Enter the number: 13 13 is a happy number
Time Complexity: O(n*log(n))
Space Complexity: O(1)
Conclusion
Happy numbers are special numbers that give the value 1 when we constantly replace them with the sum of the square of their digits. There are three methods that we have discussed to find out if a number is happy or not, the naive approach, the less space approach, and the alternative method.