Recursion is a powerful technique in programming that allows a function to call itself. In Java, recursion can be used to solve complex problems by breaking them down into simpler subproblems. In this comprehensive guide, we well explore the concept of recursion in Java, its advantages and disadvantages, and examine several real-world examples of recursion in action.
What is Recursion?
Recursion is a process in which a function calls itself, either directly or indirectly. It involves breaking down a complex problem into smaller, more manageable subproblems until a base case is reached. The base case represents the simplest form of the problem and allows the recursion to terminate. Each recursive call works towards solving the problem by reducing it to a smaller subproblem.
One key aspect of recursion is the presence of a stop condition or base case. The base case defines the condition under which the recursion should stop and the function should return a result. Without a base case, the recursive function would continue to call itself indefinitely, leading to a stack overflow error.
Another important element of recursion is the recursive call. This is the part of the function where it calls itself with a modified input that brings it closer to the base case. The recursive call allows the function to work towards solving the problem by breaking it down into simpler subproblems.
If your primary language is C++, you can check out this article: Recursion in C++
Tail Recursion vs Head Recursion
Recursion can be categorized into two types: tail recursion and head recursion. In tail recursion, the recursive call is the last operation performed within the function. This means that there is no need to perform any additional operations after the recursive call. Tail recursion is considered more efficient as it allows for potential optimization by the compiler or interpreter.
On the other hand, head recursion occurs when the recursive call is not the last operation in the function. In head recursion, there are additional operations to be perform efter the recursive call. While head recursion is still a valid form of recursion, it may require more memory as each recursive call adds a new frame to the stack.
It is important to note that while some programming languages, such as Scheme, optimize tail recursion, Java does not currently provide tail-call optimization. Therefore, it is a good practice to be mindful of the potential memory usage when implementing recursive solutions in Java.
Recursion vs Iteration
Recursion and iteration (using loops) are two primary approaches to problem-solving in programming. Both have their advantages and disadvantages.
Advantages of Recursion:
- Elegant Code: Recursion can lead to concise and elegant code for problems with recursive structures.
- Divide and Conquer: It's well-suited for problems that can be divided into smaller, similar subproblems.
- Readability: Recursive code often mirrors the problem's natural recursive definition, making it more readable.
Advantages of Iteration:
- Efficiency: Iterative solutions can be more efficient in terms of time and memory usage for certain problems.
- Predictability: Loops provide control over the flow of execution, making them predictable and potentially easier to optimize.
If you want to learn more differences between Recursion and Iteration. Check out this: Recursion Vs Iteration.
Example 1: Summing a Series of Numbers
Let's begin by exploring a simple example of recursion in Java: summing a series of numbers.
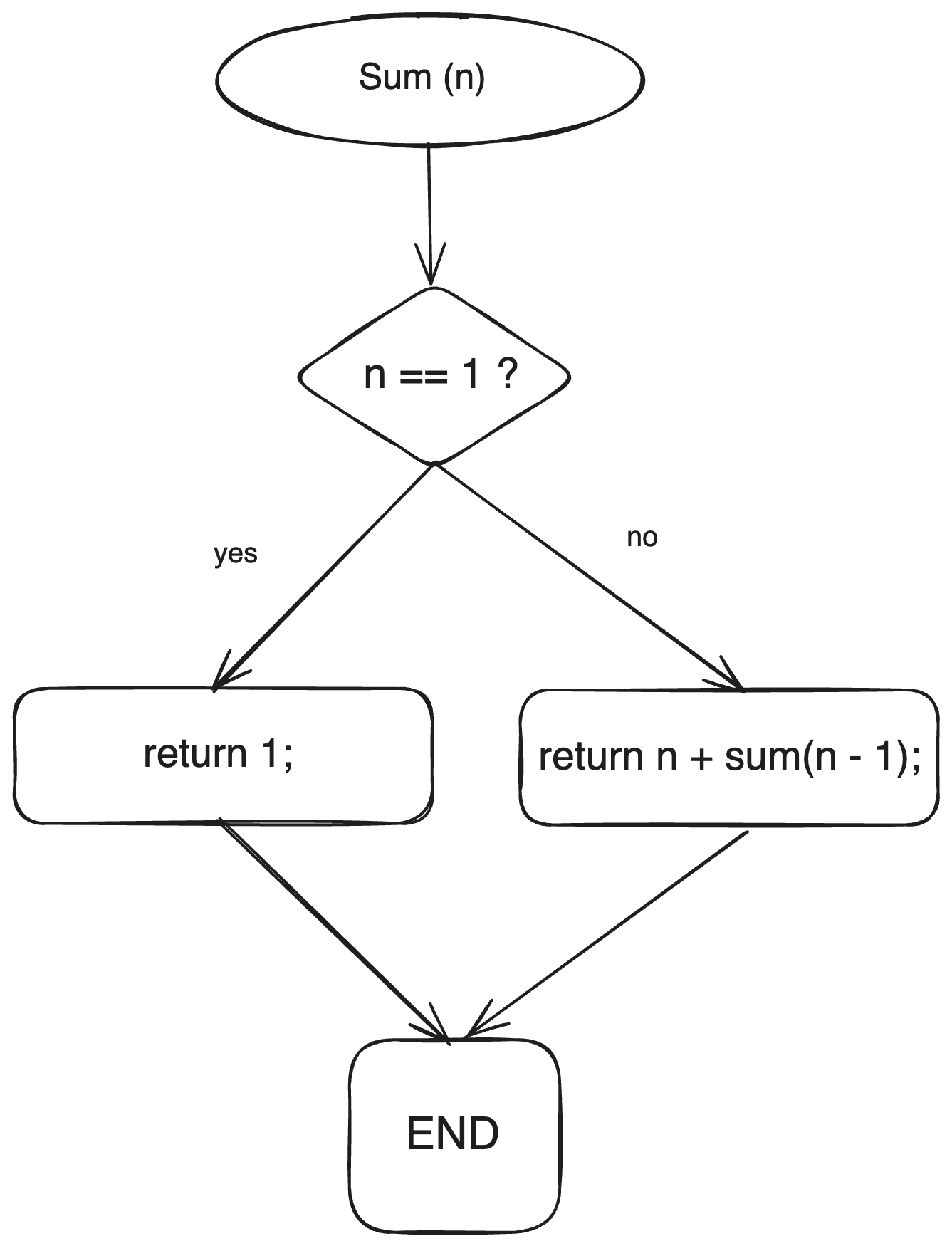
Suppose we want to calculate the sum of all integers from 1 to a given number, n. We can solve this problem recursively by breaking it down into smaller subproblems.
public class RecursiveSum { public static int sum(int n) { if (n == 1) { return 1; } return n + sum(n - 1); } }
In this example, the sum method takes an integer n as input and recursively calculates the sum of all integers from n to 1. The base case occurs when n is equal to 1, in which case the method simply returns 1. Otherwise, the method adds n to the sum of all integers from n-1 and returns the result.
Let's test our sum method with a few sample inputs:
public static void main(String[] args) { System.out.println(RecursiveSum.sum(5)); // Output: 15 System.out.println(RecursiveSum.sum(10)); // Output: 55 System.out.println(RecursiveSum.sum(20)); // Output: 210 }
As you can see, the sum method uses recursion to efficiently calculate the sum of a series of numbers.
Example 2: Calculating Factorials
Factorial is another classic example that can be solved using recursion.
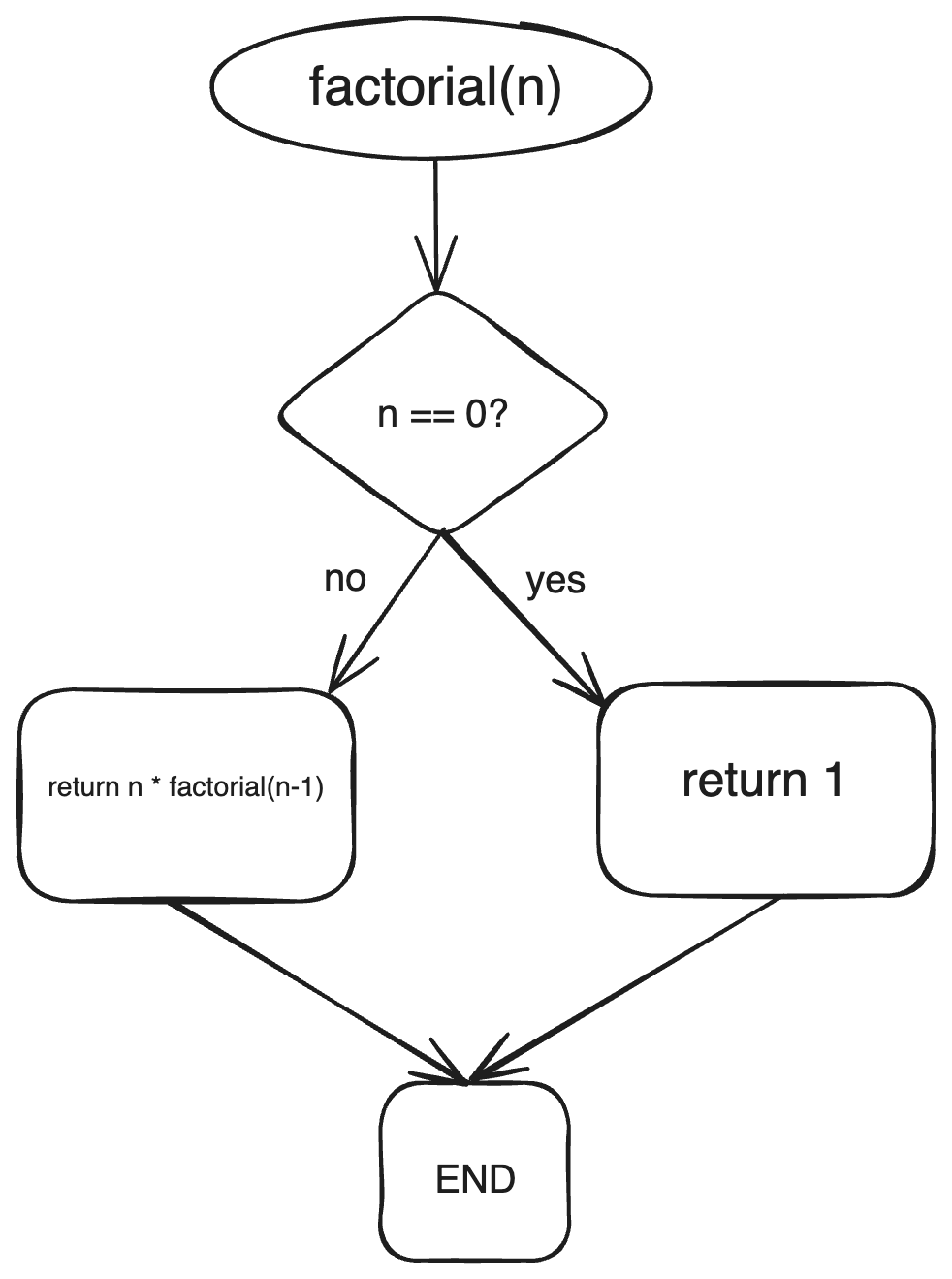
The factorial of a non-negative integer n, denoted as n!, is the product of all positive integers from 1 to n. We can calculate the factorial of n recursively by defining the base cast as n = 0, where the factorial is 1, and using the recursive formula n! = n * (n-1)!.
public class RecursiveFactorial { public static int factorial(int n) { if (n == 0) { return 1; } return n * factorial(n - 1); } }
In this example, the factorial method takes an integer n as input and calculates the factorial of n using recursion. The base case occurs when n is equal to 0, in which case the method returns 1. Otherwise, the method multiplies n with the factorial of n-1 and returns the result.
Let's test our factorial method with a few sample inputs:
public static void main(String[] args) { System.out.println(RecursiveFactorial.factorial(5)); // Output: 120 System.out.println(RecursiveFactorial.factorial(8)); // Output: 40320 System.out.println(RecursiveFactorial.factorial(10)); // Output: 3628800 }
As you can see, the factorial method uses recursion to calculate the factorial of a given number.
Example 3: Generating Fibonacci Sequence
Let's take anothe example.
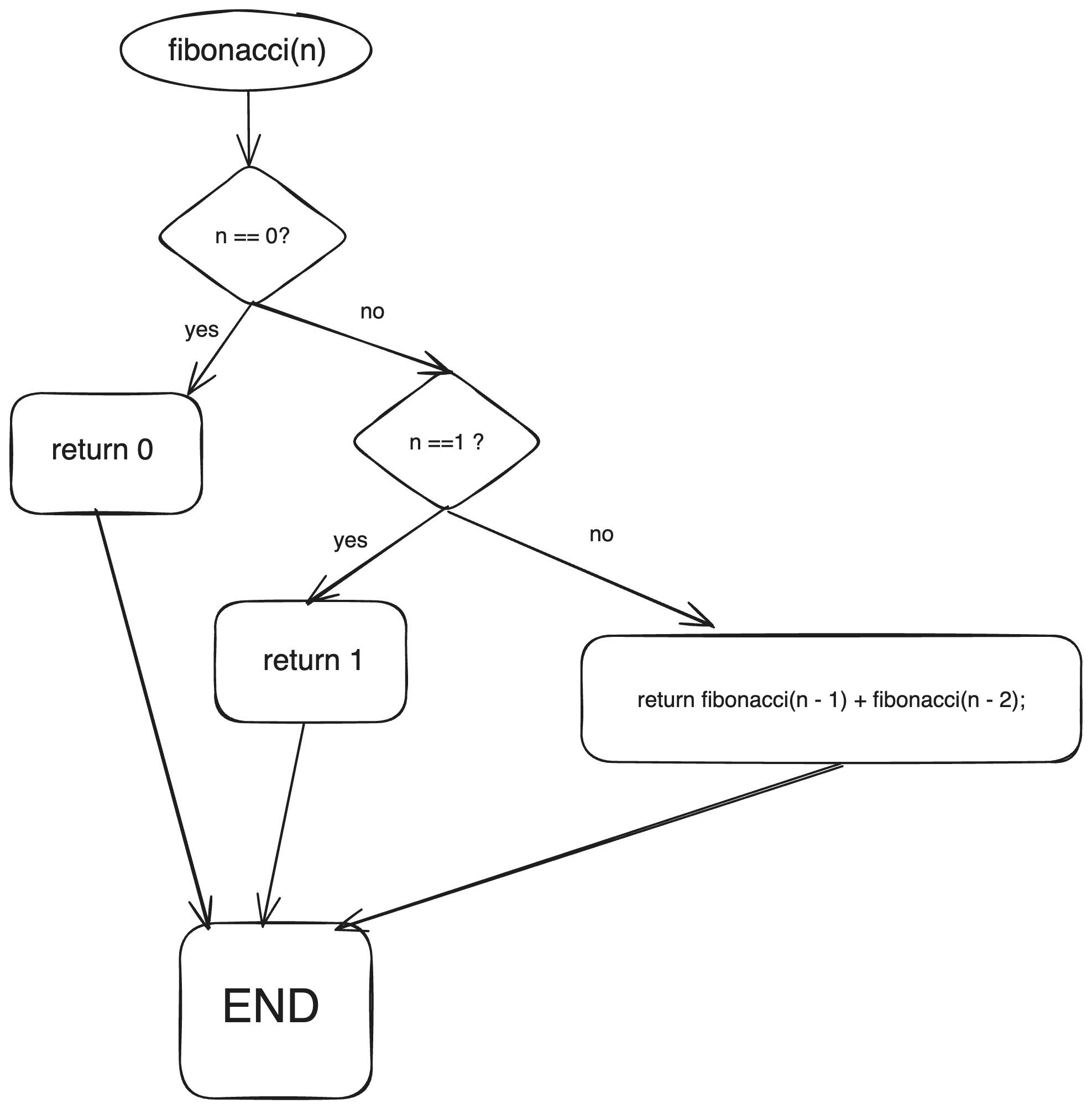
The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. The sequence starts with 0 and 1, and the subsequent numbers are obtained by adding the previous two numbers. We can generate the Fibonacci sequence recursively by defining the best cases as n = 0 and n = 1, where the sequence is simply 0 and 1, respectively, and using the recursive formula fib(n) = fib(n-1) + fib(n-2) for n > 1.
public class RecursiveFibonacci { public static int fibonacci(int n) { if (n == 0) { return 0; } if (n == 1) { return 1; } return fibonacci(n - 1) + fibonacci(n - 2); } }
In this example, the fibonacci method takes an integer n as input and generates the n-th number in the Fibonacci sequence using recursion. The best cases occur when n is equal to 0 or 1, in which case the method simply returns 0 or 1, respectively. Otherwise, the method calculates the n-th number by adding the (n-1)-th and (n-2)-the numbers in the sequence.
Let's test our fibonacci method with a few sample inputs:
public static void main(String[] args) { System.out.println(RecursiveFibonacci.fibonacci(6)); // Output: 8 System.out.println(RecursiveFibonacci.fibonacci(8)); // Output: 21 System.out.println(RecursiveFibonacci.fibonacci(10)); // Output: 55 }
As you can see, the fibonacci method uses recursion to generate the n-th number in the Fibonacci sequence.
Example 4: Converting Decimal to Binary
Let's see how can we convert decimal to binary.
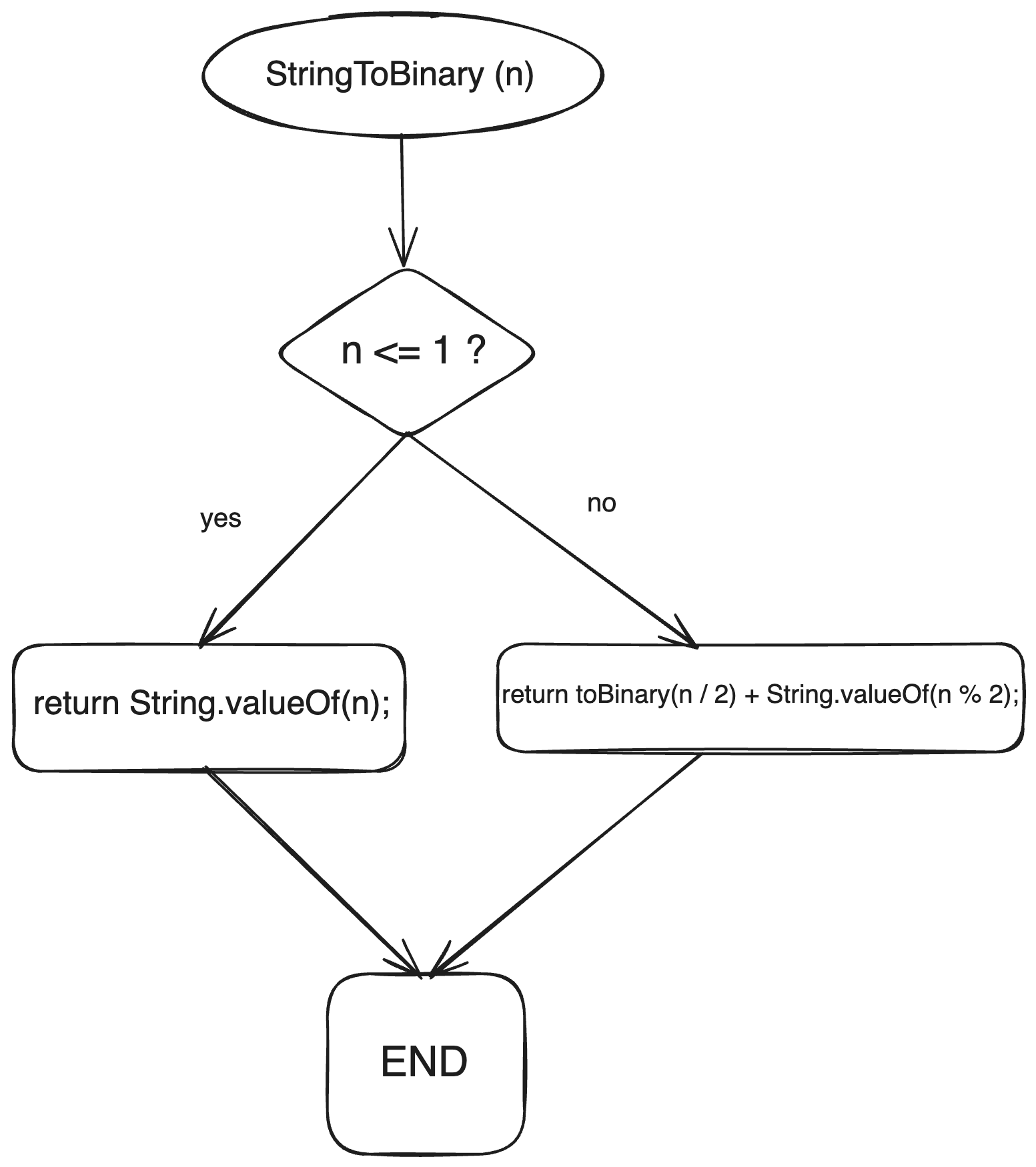
Converting a decimal number to its binary representation is another problem that can be solved using recursion. One approach to convert a decimal number to binary is to repeatedly divide the number by 2 and record the remainder. This process continues until the quotient becomes 0. The binary representation of the decimal number can then be obtained by concatenating the remainder in reverse order.
public class RecursiveBinaryConversion { public static String toBinary(int n) { if (n <= 1) { return String.valueOf(n); } return toBinary(n / 2) + String.valueOf(n % 2); } }
In this example, the toBinary method takes an integer n as input and recursively converts it to its binary representation. The base case occurs when n is less than or equal to 1, in which case the method simply returns the string representation of n. Otherwise, the method divides n by 2 and recursively calls itself with the quotient, while also appending the remainder to the result.
Let's test our toBinary method with a few sample inputs:
public static void main(String[] args) { System.out.println(RecursiveBinaryConversion.toBinary(10)); // Output: 1010 System.out.println(RecursiveBinaryConversion.toBinary(23)); // Output: 10111 System.out.println(RecursiveBinaryConversion.toBinary(37)); // Output: 100101 }
As you can see, the toBinary method uses recursion to convert a decimal number to its binary representation.
Recursion in Data Structures
Recursion is not limited to function calls; it can also be applied to data structures. Some data structures, such as linked lists and trees, have recursive definitions that lend themselves well to recursive manipulation.
Let's take a look at using recursion in traversing a binary tree:
// Recursive Binary Tree Traversal class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int val) { this.val = val; } } public class BinaryTreeTraversal { public static void inOrderTraversal(TreeNode node) { if (node != null) { inOrderTraversal(node.left); System.out.print(node.val + " "); inOrderTraversal(node.right); } } public static void main(String[] args) { TreeNode root = new TreeNode(1); root.left = new TreeNode(2); root.right = new TreeNode(3); root.left.left = new TreeNode(4); root.left.right = new TreeNode(5); System.out.print("In-Order Traversal: "); inOrderTraversal(root); } }
Output:
In-Order Traversal: 4 2 5 1 3
This example demonstrates how recursion is used to traverse a binary tree.
The Concept of Tail Recursion
Tail recursion is a specific form of recursion in which the recursive call is the last operation in a function. In Java, tail-recursive functions can be optimized by the compiler through a process called "tail call optimization."
Here's an example of a tail-recursive function to calculate the factorial of a number:
public class TailRecursionExample { public static int factorialTailRecursive(int n, int result) { if (n == 0) { return result; } return factorialTailRecursive(n - 1, n * result); } public static int factorial(int n) { return factorialTailRecursive(n, 1); } public static void main(String[] args) { int n = 5; int result = factorial(n); System.out.println(n + "! = " + result); } }
In this example, the factorialTailRecursive function is tail-recursive, and the compiler can optimize it.
Output:
5! = 120
Tail recursion is an essential concept for understanding how certain recursive functions can be optimized.
Advantages and Disadvantages of Recursion
Recursion offers several advantages and disadvantages in the context of programming.
Advantages of Recursion
- Simplicity: Recursion can lead to more concise and readable code, making it easier to understand and maintain.
- Problem-solving: Recursion allows us to break down complex problems into simpler subproblems, making it an effective approach for certain types of problems.
- Mathematical elegance: Recursion often aligns well with mathematical concepts and formulas, enabling the translation of mathematical problems into elegant recursive solutions.
Disadvantages of Recursion
- Memory usage: Recursive solutions may require more memory compared to iterative solutions, as each recursive call adds a new frame to the stack.
- Performance: Recursion can be less efficient than iteration in terms of performance, especially for large inputs, due to the overhead of function calls and stack management.
- Stack overflow: If not implemented carefully, recursion can lead to stack overflow errors when the recursion depth exceeds the maximum stack size.
It is important to consider these advantages and disadvantages when deciding whether to use recursion in a specific problem-solving scenario. While recursion can offer elegent and concise solutions, it may not always be the most efficient or practical approach.
Conclusion
Recursion is a powerful concept in programming that allows a function to call itself, enabling the solution of complex problems by breaking them down into simpler subproblems. In this comprehensive guide, we explorer the fundamentals of recursion in Java, including its definition, characteristics, and advantages and disadvantages. We also examined several real-world examples of recursion, such as summing a series of numbers, calculating factorials, generating Fibonacci sequences, converting decimal to binary, and calculating the height of a binary tree.