Longest Common Prefix ( With C++, Java and Python Code)

Companies like Amazon, Facebook, and Microsoft frequently use the competitive question as part of the technical interview to assess candidates' conceptual expertise. The longest common prefix problem is one of those competitive problems that you must master in order to land a job at your dream firm. In this article, we will study the longest common subsequence or LCS problem and the approach to solve it using python, java, C++ code, and output. Let’s get started!

What is Longest Common Prefix Problem?

Let us first understand this problem in detail before moving to the approach.

‘Given a set of strings, find the longest common prefix '.

We will now look at an example to understand this better. Suppose we have been given three strings: Favtutor, Favourite, Favour. The longest common subsequence, in this case, will be Fav. Let us take another example, but now the strings given to us are apple, orange, banana. In this case, “ ” or null string should be returned. Great! Now we understand the problem statement, let us move on to the approach.

How to Find the Longest Common Prefix?

In this article, we discuss the Brute- Force approach to search for the LCP. In this approach, we match each character of one string with the corresponding characters of other strings hence this approach can also be known as the character to character matching approach. Let us now look at the working of this approach in a little more detail.

In this approach, we maintain a counter variable and initialize it 0, indicating that no common prefix exists initially. Apart from this, we also maintain a result variable, which will store the longest common subsequence. Next, run the loop from 0 to the length of the string with minimum length and later, in each iteration, compare the characters of all strings at the index equal to the iteration value. Confusion right?  Don’t worry, we got your back.

Let us start from the beginning, In the first iteration, the first index of all the strings will be compared. Similarly in the second iteration, the second index of all the strings will be compared and so. Now if the comparison evaluates to be “equal” then we increment the counter by 1 and concatenate the character compared in this iteration to result string. Now, if in any iteration the comparison evaluates to be “not equal”, then the loop breaks and we get our LCP stored in the result string.

To solidify what we discussed in the previous discussion, let us take an example to illustrate the concept.

Example

In this example, we are provided with 4 Strings: Favtutor, Favour, Favourite, Favonian. Out of all these given strings, “Favour” has a minimum length equal to 6. Therefore, our loop will run 6 times. In the first iteration, the 0th index of all the strings is compared. All 4 strings contain the same value at their 0th index, therefore we will increment the counter and concatenate the letter F with the result String.

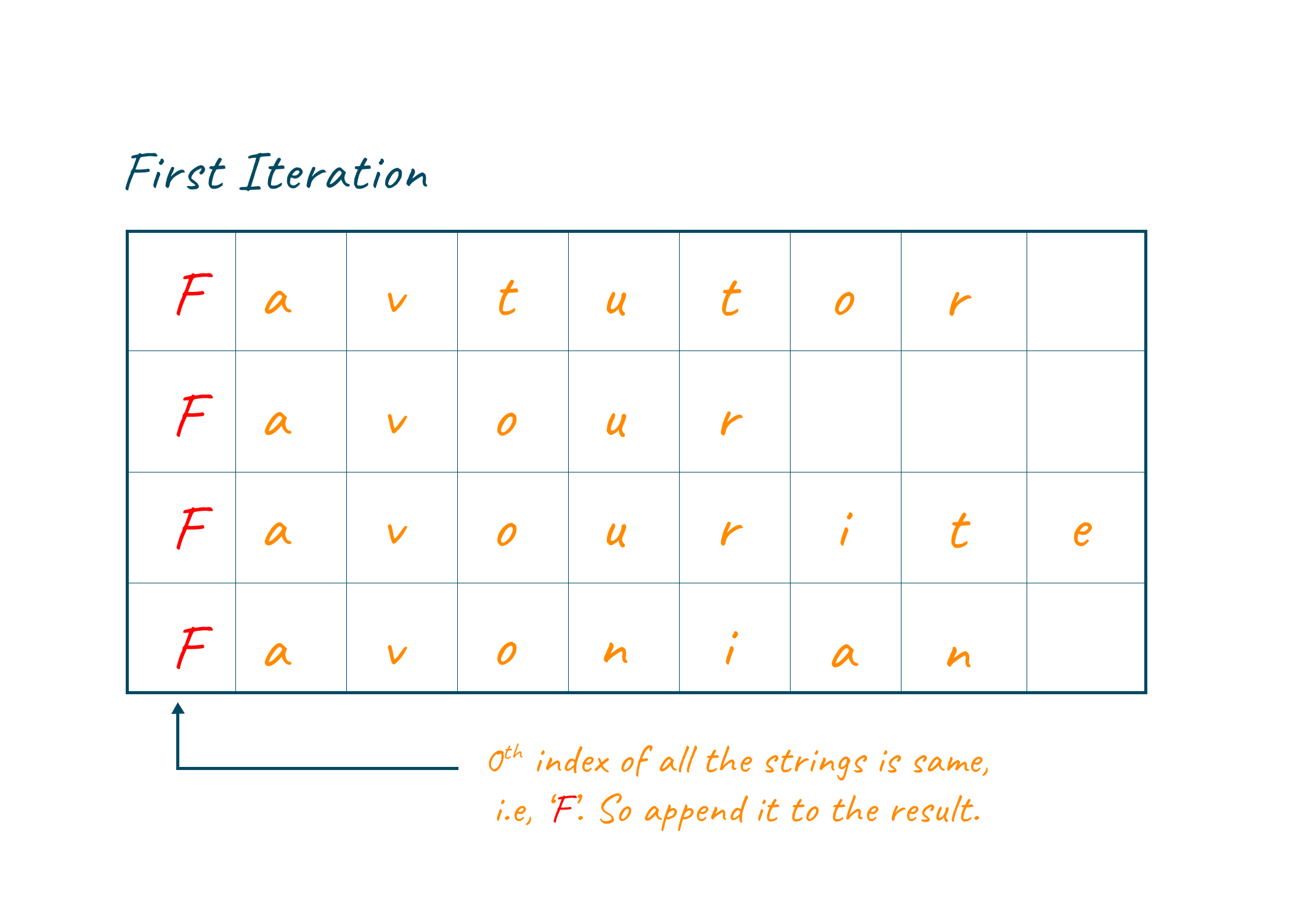
Now in this second iteration, the 1st index of all the strings is compared. In this case, also the comparison is evaluated to be true, hence the counter increments by 1, and character a is concatenated with the result.

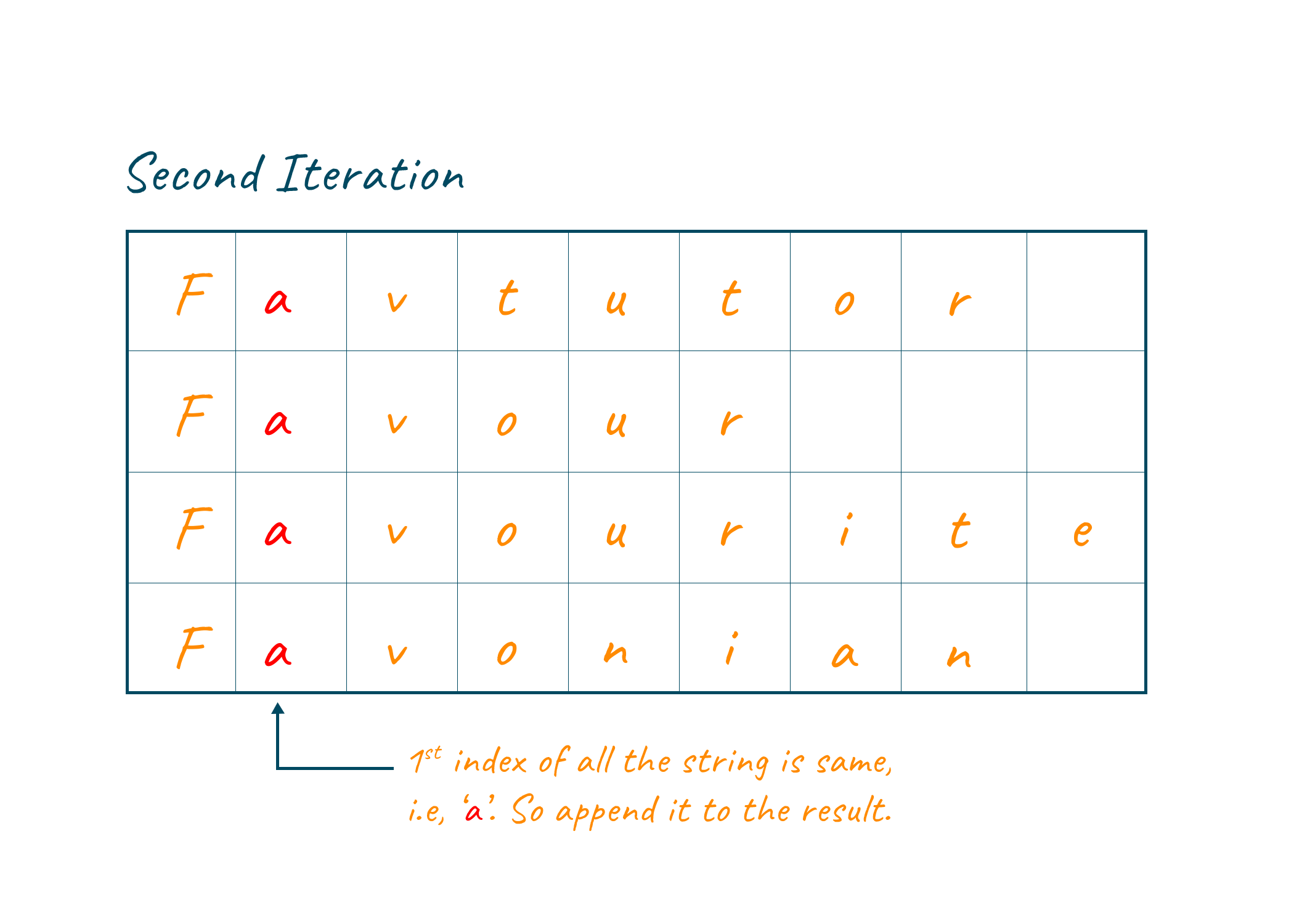
In the third iteration, the 2nd index is compared, and the comparison evaluates to true. The counter is incremented and the letter v is concatenated with the result string.

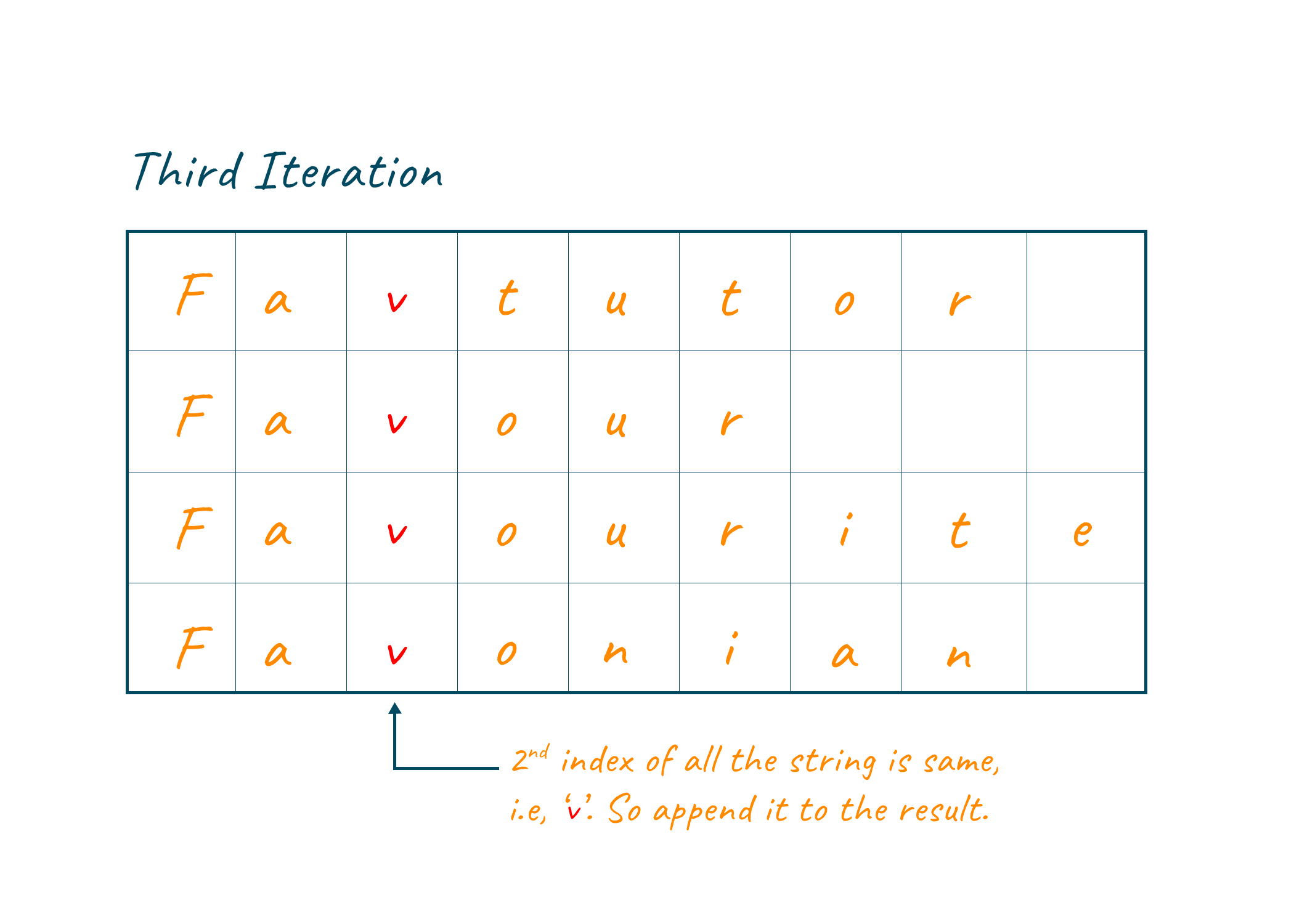
In the fourth iteration, we compare the 3rd index of the string. Since Favtutor contains 't' at its 3rd index and the rest of all strings contain o, the comparison evaluates to be false. The loop terminates and we get “Fav” as the longest common prefix.

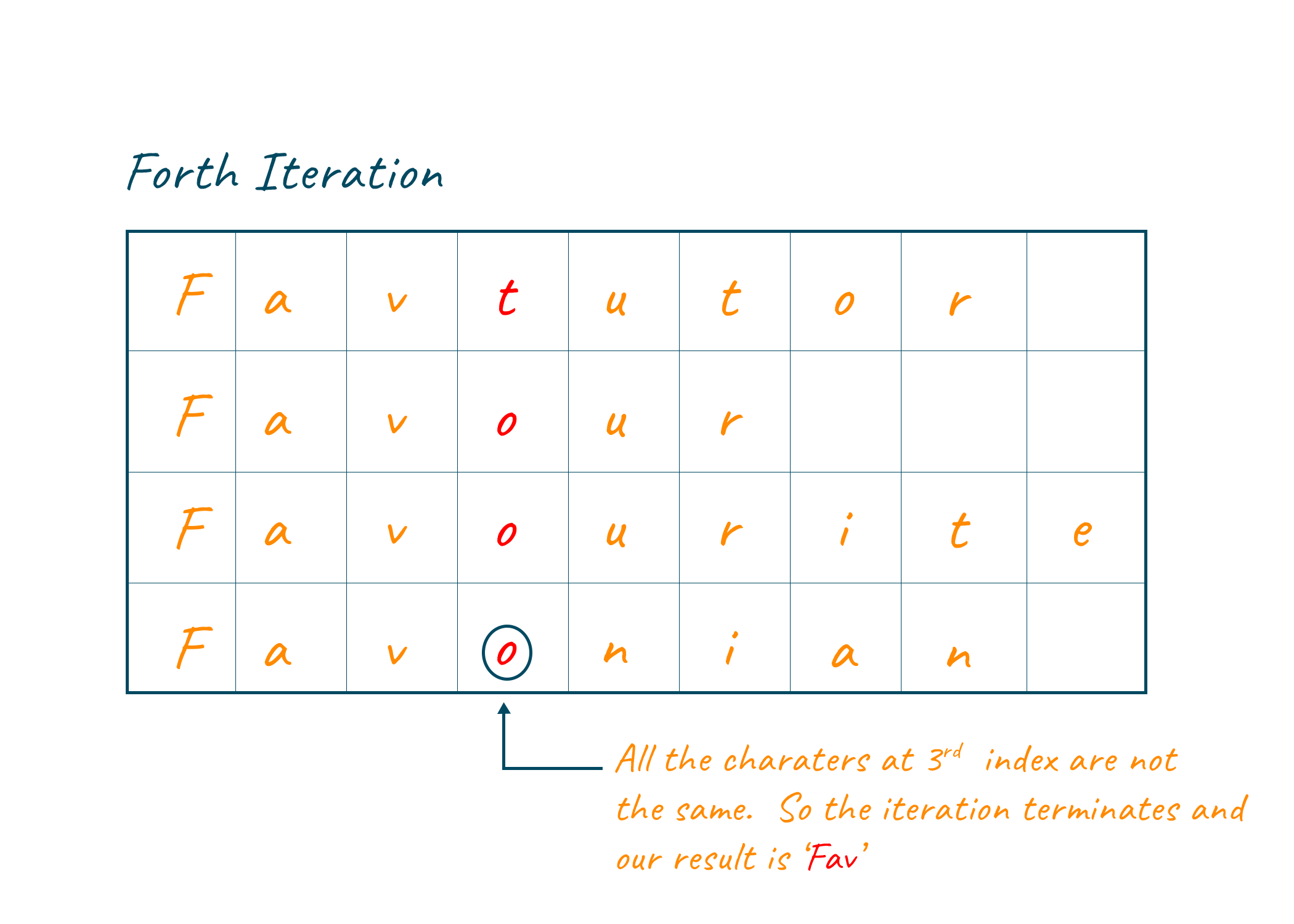
Solution of Longest Common Prefix

Let us now look at the code implementing the brute force approach for finding the longest common prefix. Since, in reality, we do not know how many strings will be provided to us, therefore, we use nested loops: the outer loop runs equal to the minimum length of the string and the inner loop runs for each string. It is the inner loop inside which the comparison takes place.

Java code for longest common prefix

class favtutor {
    public String longestCommonPrefix(String[] strs) {

        String ans="";
        int n= strs.length;

        int min= Integer.MAX_VALUE;
        for(int i=0;i<n;i++){

            int len= strs[i].length();
            min= Math.min(min,len);
        }


        for(int i=0;i<min;i++){

            char x1= strs[0].charAt(i);
            boolean possible=true;
            for(int j=1;j<n;j++){

                if(strs[j].charAt(i)!=x1){
                    possible=false;
                    break;
                }
            }
            if(possible){
                ans+=x1;
            }
            else{
                break;
            }
        }
        return ans;
    }
}

C++ code for longest common prefix

#include<bits/stdc++.h>
using namespace std;

// A Function to find the string having the minimum length and returns that length
int findMinLength(int n, vector<string> &strs)
{
	int minLen = strs[0].length();

	for (int i = 1; i < n; i++)
		if (strs[i].length() < minLen)
			minLen = strs[i].length();

	return minLen;
}
// A Function that returns the longest common prefix from the vector of strings
string longestCommonPrefix(int n, vector<string>& strs) {

	// if vector of strings is empty, return empty string
	if (n == 0)
		return "";
	string ans = "";		// our answer string
	int minLen = findMinLength(n, strs);

	for (int i = 0; i < minLen; i++)
	{
		// Current character (must be same in all strings to be a part of result)
		char ch = strs[0][i];
		for (int j = 0; j < n; j++)
		{
			if (ch != strs[j][i])
				return ans;
		}
		// Append the current character in our answer string
		ans.push_back(ch);
	}
	return ans;
}
int main()
{
	int n;
	cin >> n;
	vector<string> strs(n);
	for (int i = 0; i < n; i++) cin >> strs[i];
	cout << longestCommonPrefix(n, strs);
}

Python code for longest common prefix

# Function to find the string having the minimum length
def findMinLength(arr, n):

    min = len(arr[0])

    for i in range(1,n):
        if (min > len(arr[i])):
            min = len(arr[i])

    return(min)

def commonPrefix(arr, n):

    minlen = findMinLength(arr, n)
    result =""
    for i in range(minlen):
    
        #Current stores the letter
        # to be compared
        current = arr[0][i]

        for j in range(1,n):
            if (arr[j][i] != current):
                return result

        # Append to result
        result = result+current

    return (result)

    
arr = ["Favtutor", "Favour", "Favourite", "Favonian"]
n = len(arr)
# Find the LCP using a function
ans = commonPrefix (arr, n)
# Print the LCP
print("The longest common prefix is ",ans)

Output:

The longest common prefix is  Fav 

Time Complexity

Let m be the length of the smallest string and n be the number of strings. In the worst case, the outer loop can run m times, and the inner loop runs n times. Therefore, the time complexity of this approach is O(N*M).

Space Complexity

Since the only space required to solve the longest common subsequence is the maximum length of the smallest string, the space complexity of this approach results to O(M) where M is the length of the smallest string. 

Conclusion

Solving competitive problems like these strengthen one's brain and improves problem-solving abilities. In this article, we discussed the longest common prefix problem along with its solution, example, and respective code. Note that the solution discussed today is the simplest one and that this problem can be solved using some other approach as well.