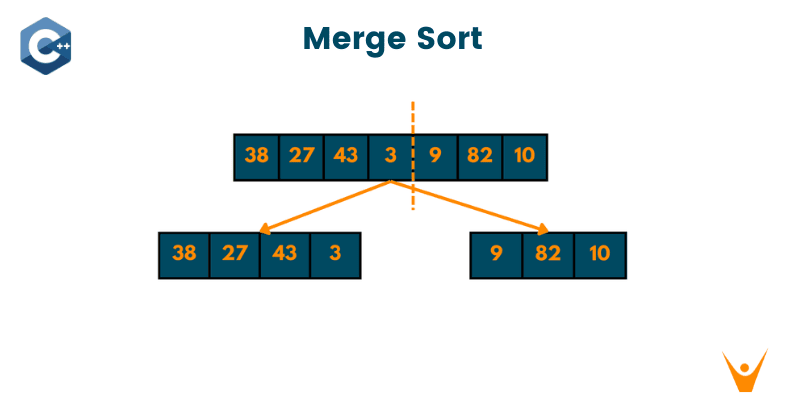
Sorting is one of the most basic concepts programmers need to learn and Merge Sort is a must to crack the technical interviews. In this article, we will discuss Merge Sort, its algorithm, implementation with C++ program, and time complexity. So, Let's get started!
What is Merge Sort?
Imagine you have a bunch of blocks, and you want to sort them from smallest to biggest. But you can only compare two blocks at a time. What do you do? You can split the blocks into two groups, and sort each group separately.
Once you have two sorted groups, you can compare the smallest block from each group and put the smaller one first in a new group. Then you can compare the next smallest blocks, and keep adding them to the new group in order.
You keep doing this until all the blocks are in the new group, and they are all in order from smallest to biggest! This is what merge sort does with numbers in a computer. So merge sort is a way to sort things by dividing them into smaller groups, sorting each group, and then putting them all back together in the right order. It's like sorting toys but for a computer!
Merge sort is a widely used sorting algorithm that utilizes the divide-and-conquer technique to sort an array. It has a time complexity of O(nlogn), making it one of the most efficient sorting algorithms, particularly for large data sets.
The basic idea for it is to repeatedly divide the unsorted list into two halves until we have individual elements. Then, we merge these elements in sorted order until the entire list is sorted.
Before discussing more, we need to discuss the divide and conquer algorithm.
Divide and Conquer Algorithm
Divide and conquer is a problem-solving technique that involves breaking down a big problem into smaller, more manageable subproblems, solving each subproblem independently, and then combining the solutions to solve the original problem.
The basic idea behind divide and conquer is to divide the problem into smaller subproblems that are easier to solve, and then to combine the solutions of the subproblems as a means of obtaining the answer to the initial question. This approach can be used to solve a wide range of problems, from simple arithmetic problems to complex optimization problems.
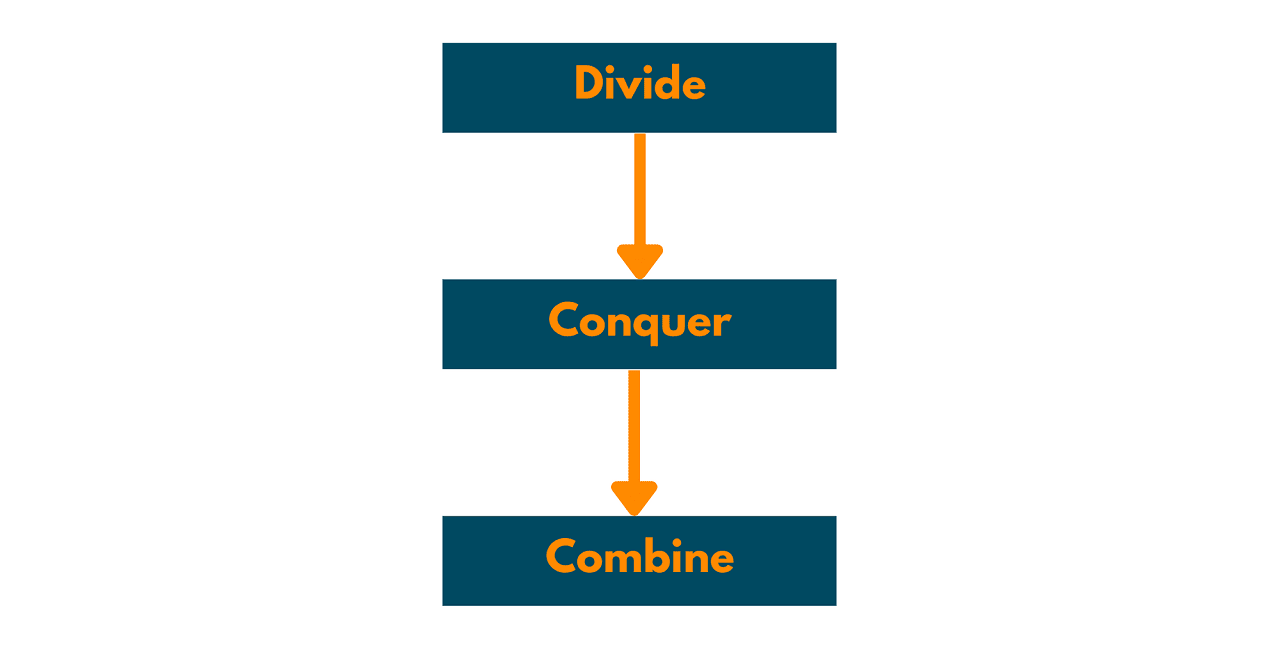
To use divide and conquer, we typically follow these steps:
- Divide the problem into smaller subproblems that are easier to solve.
- Solve each subproblem independently using a recursive approach.
- Combine the subproblem answers together to yield the answer to the main problem.
Divide and conquer can be a very effective approach for solving problems because it can help us to break down complex problems into simpler, more manageable pieces. By solving each piece independently and then combining the solutions, we can often arrive at a more efficient and effective solution to the original problem.
Working Principle of Merge Sort
Merge sort divides the input array into two halves, and then each half is recursively divided until we have subarrays of only one element. These subarrays are then merged in pairs in a sorted manner until we have only one sorted array.
The merge step is the core operation of the Merge sort. In this step, two sorted arrays are combined into a single sorted array. The merge step works by comparing the elements of the two sorted subarrays and placing the smaller element into a new array.
This process continues until one of the subarrays is completely merged into the new array. The remaining elements from the other subarray are then added to the new array.
Merge Sort Algorithm
The basic steps of merge sort are as follows:
- Divide the input array into two halves, until each subarray contains only one element.
- Merge the subarrays by comparing the first element of each subarray and placing the smaller element in a new array.
- Repeat step 2 until one of the subarrays has been completely merged into the new array.
- Copy the remaining elements from the other subarray into the new array.
- The new array is now a sorted version of the input array.
The merge operation requires additional memory to create a new array. Therefore, Merge sort may be less efficient in terms of space complexity compared to other sorting algorithms. However, the time complexity of Merge sort is significantly better than other sorting algorithms, particularly for large data sets.
Merge Sort Example
Let's say we have an array of numbers that we want to do sorting using Merge Sort:

Divide the array into two halves
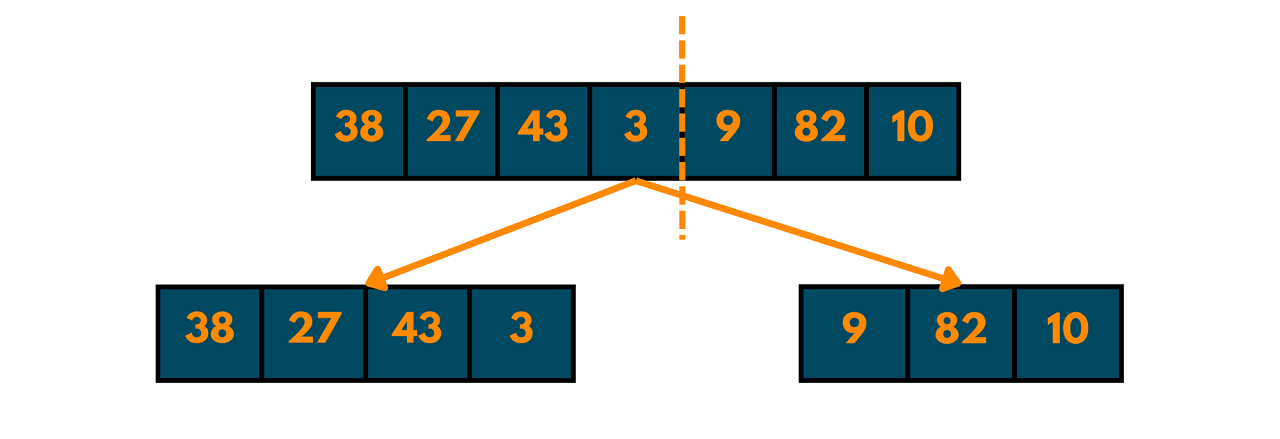
Keep dividing until each element is a separate list
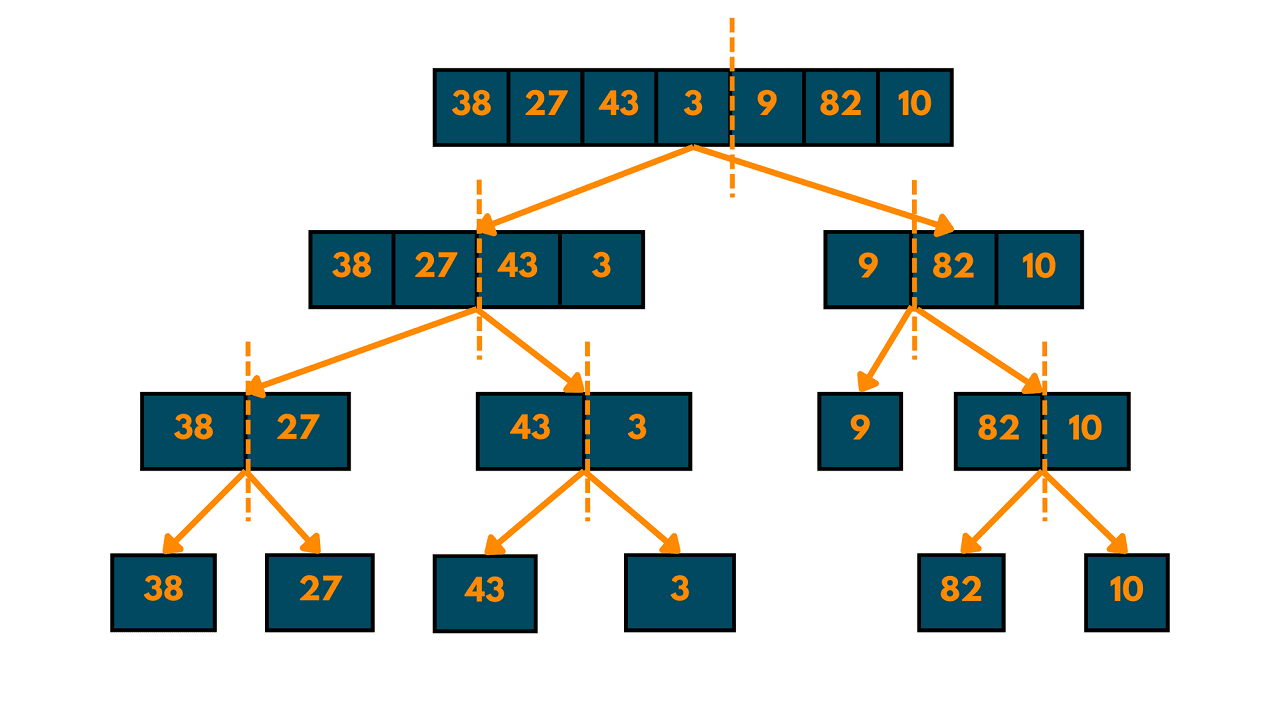
Start merging the elements from two sorted halves
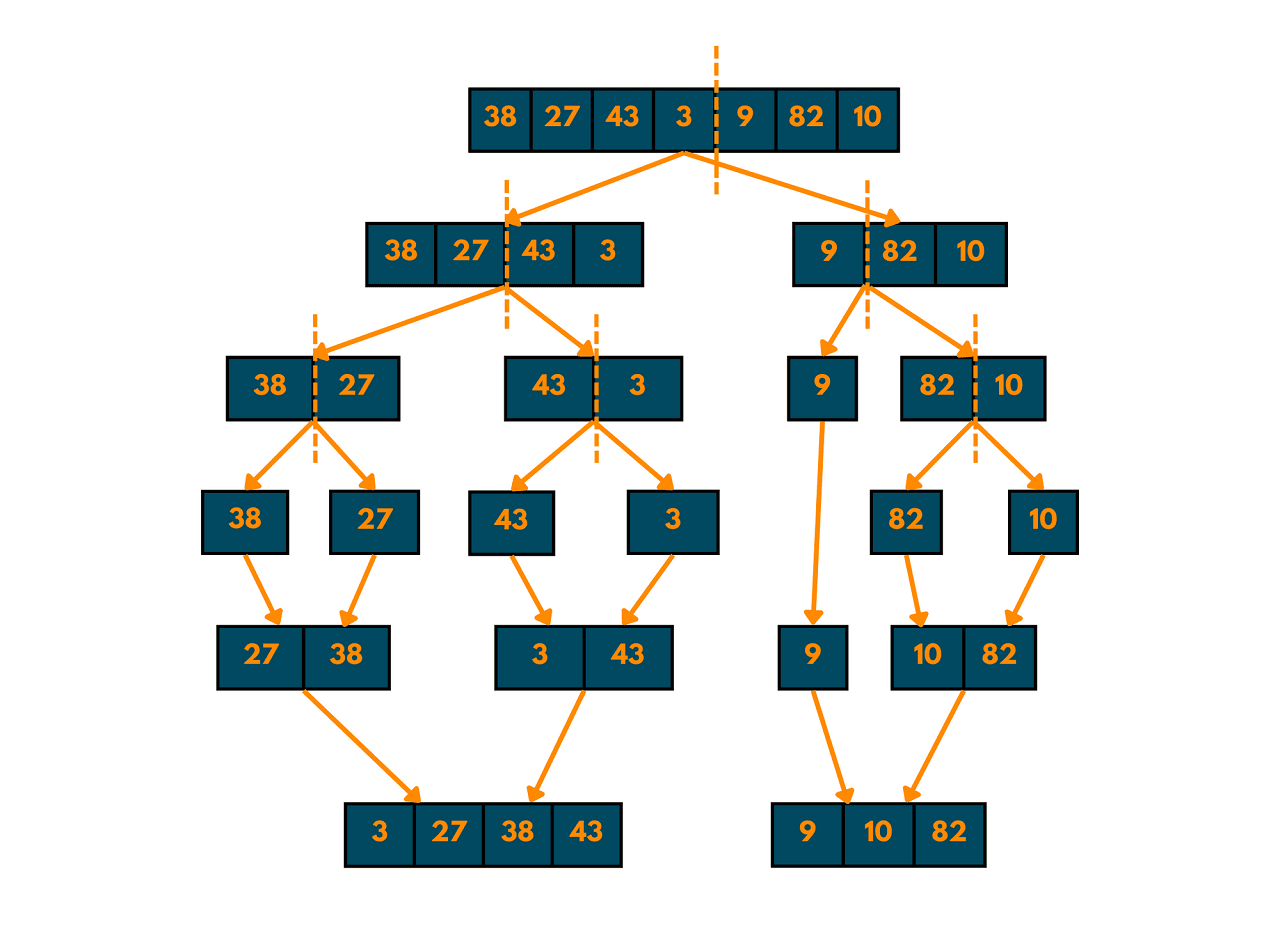
Merge the two sorted halves
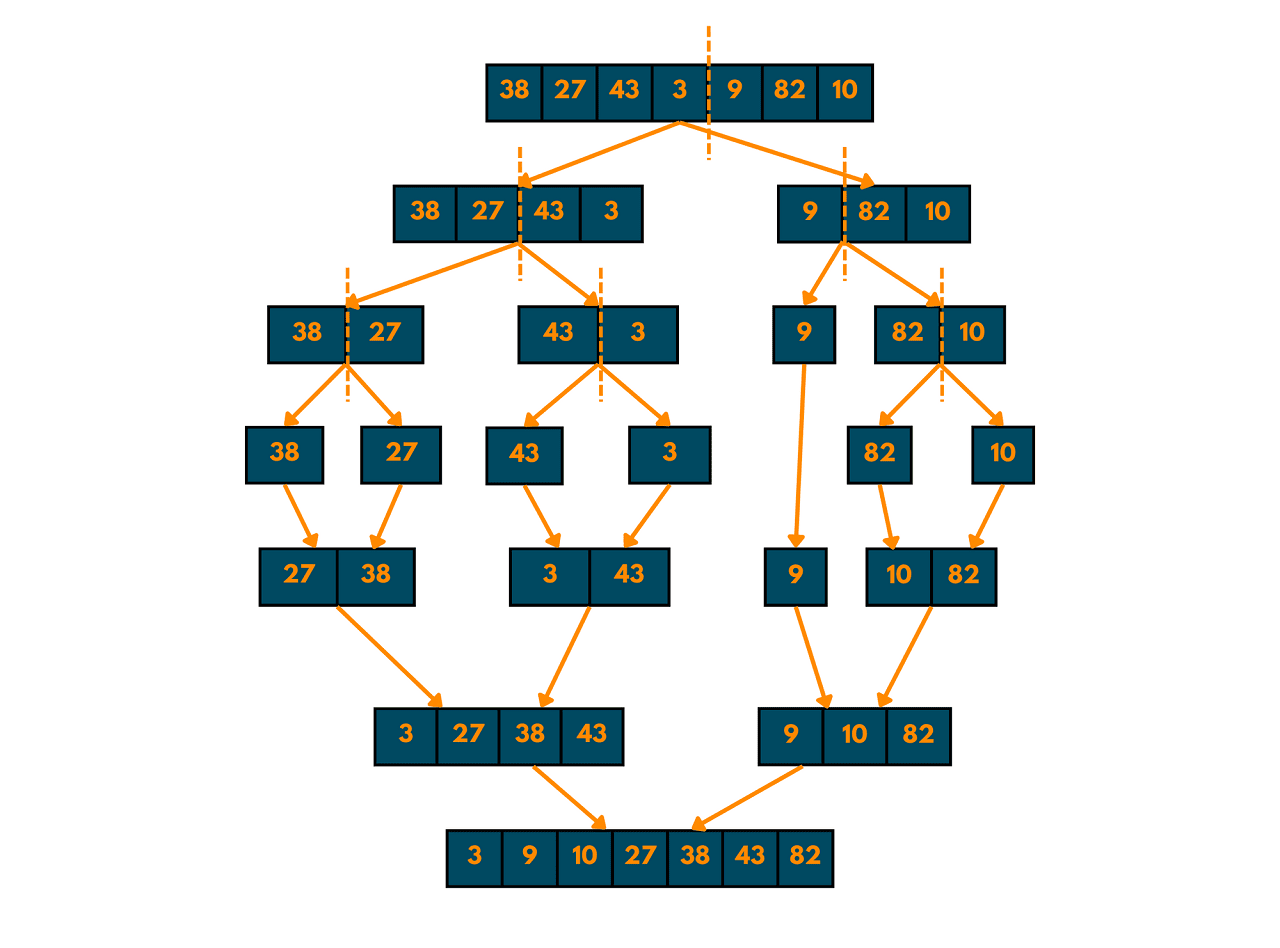
And there we have it! The array is now sorted in ascending order. This is the basic idea behind Merge Sort, which is to recursively divide the array into smaller subarrays, sort each subarray, and then merge the sorted subarrays together.
C++ Pseudocode
Here we can have a look at the pseudocode of merge sort because we understand the code in C++:
MergeSort(array, left, right): if left >= right return mid = left + (right-left)/2 mergeSort(array, left, mid) mergeSort(array, mid+1, right) Form the leftArray Form the rightArray merge(array, leftArray, mid - left + 1, rightArray, right - mid)
Time Complexity
The time complexity of the Merge sort for the best, worst, and average case is O(nlogn), where n is the size of the input array. This makes Merge sort one of the most efficient sorting algorithms, particularly for large data sets.
Merge sort divides the input array into smaller subarrays, and each subarray is sorted separately. The merge step requires time proportional to the size of the two subarrays being merged, and this operation is performed for each pair of subarrays.
Because the sorting technique used by merge sort is stable, it preserves the relative order of identical elements in the input array. This makes Merge sort a popular choice for sorting objects with multiple attributes, where it is important to preserve the order of attributes.
Also, the space complexity is O(N), where N is the size of the input array.
C++ Implementation for Merge Sort
There are two ways to implement Merge Sort in C++: Recursive and Iterative. Let's discuss both of them one by one.
Recursive Merge Sort
Recursive Merge Sort is an efficient sorting algorithm that uses a divide-and-conquer approach to sort an array of elements. It divides the array into two halves, sorts the two halves recursively, and then merges them into a single sorted array. Here is an implementation of Recursive Merge Sort in C++:
#include using namespace std; // Merge function to merge two sorted arrays void merge(int arr[], int left[], int leftSize, int right[], int rightSize) { int i = 0, j = 0, k = 0; while (i < leftSize && j < rightSize) { if (left[i] <= right[j]) { arr[k++] = left[i++]; } else { arr[k++] = right[j++]; } } while (i < leftSize) { arr[k++] = left[i++]; } while (j < rightSize) { arr[k++] = right[j++]; } } // Recursive Merge Sort function to sort the array void recursiveMergeSort(int arr[], int left, int right) { if (left >= right) { return; } int mid = left + (right - left) / 2; recursiveMergeSort(arr, left, mid); recursiveMergeSort(arr, mid + 1, right); int leftArr[mid - left + 1], rightArr[right - mid]; for (int i = 0; i <= mid - left; i++) { leftArr[i] = arr[left + i]; } for (int i = 0; i < right - mid; i++) { rightArr[i] = arr[mid + 1 + i]; } merge(arr, leftArr, mid - left + 1, rightArr, right - mid); } // Driver code to test the Recursive Merge Sort function int main() { int arr[] = { 38, 27, 43, 3, 9, 82, 10 }; int size = sizeof(arr) / sizeof(arr[0]); cout << "Original array:" << endl; for (int i = 0; i < size; i++) { cout << arr[i] << " "; } cout << endl; recursiveMergeSort(arr, 0, size - 1); cout << "Sorted array:" << endl; for (int i = 0; i < size; i++) { cout << arr[i] << " "; } cout << endl; return 0; }
Output:
Original array: 38 27 43 3 9 82 10 Sorted array: 9 9 10 82 3 82 10
Iterative Merge Sort
Iterative Merge Sort is an alternative implementation of Merge Sort that does not use recursion. Instead, it uses a bottom-up approach to sort the array by iteratively merging adjacent pairs of subarrays until the entire array is sorted. Here is an implementation of Iterative Merge Sort in C++:
#include using namespace std; // Merge function to merge two sorted arrays void merge(int arr[], int left[], int leftSize, int right[], int rightSize) { int i = 0, j = 0, k = 0; while (i < leftSize && j < rightSize) { if (left[i] <= right[j]) { arr[k++] = left[i++]; } else { arr[k++] = right[j++]; } } while (i < leftSize) { arr[k++] = left[i++]; } while (j < rightSize) { arr[k++] = right[j++]; } } // Iterative Merge Sort function to sort the array void iterativeMergeSort(int arr[], int size) { for (int currSize = 1; currSize < size ; currSize *= 2) { for (int leftStart = 0; leftStart < size - 1; leftStart += 2 * currSize) { int mid = min(leftStart + currSize - 1, size - 1); int rightEnd = min(leftStart + 2 * currSize - 1, size - 1); int left[mid - leftStart + 1], right[rightEnd - mid]; for (int i = 0; i <= mid - leftStart; i++) { left[i] = arr[leftStart + i]; } for (int i = 0; i < rightEnd - mid; i++) { right[i] = arr[mid + 1 + i]; } merge(arr, left, mid - leftStart + 1, right, rightEnd - mid); } } } // Driver code to test the Iterative Merge Sort function int main() { int arr[] = { 38, 27, 43, 3, 9, 82, 10 }; int size = sizeof(arr) / sizeof(arr[0]); cout << "Original array:" << endl; for (int i = 0; i < size; i++) { cout << arr[i] << " "; } cout << endl; iterativeMergeSort(arr, size); cout << "Sorted array:" << endl; for (int i = 0; i < size; i++) { cout << arr[i] << " "; } cout << endl; return 0; }
Output:
Original array: 38 27 43 3 9 82 10 Sorted array: 9 9 10 82 3 82 10
Advantages & Disadvantages
The biggest advantage of Merge Sort is stables sort which is efficient for large datasets. The worst-case time complexity of O(n log n), makes it one of the most efficient sorting algorithms for large datasets. This means that the time it takes to sort a list of n elements grows proportionally to n log n.
Also, since merge sort is a divide-and-conquer algorithm, it is simple to parallelize it to utilize multiple processors or cores. By dividing the input sequence into smaller sub-sequences and sorting them in parallel, it is very fast.
But there are some disadvantages as well. One is the high space complexity of O(n), which means that it requires additional memory to store the sorted sequence. So, it is expensive in terms of both time and memory usage.
One more thing to note is that Merge Sort is not an in-place sorting algorithm, which means that it cannot sort the input sequence in its original memory location without using additional memory.
Conclusion
Overall, Merge Sort in C++ is very important for every new programmer. It is used in many areas of the computer world, including Database Management Systems, Parallel Processing, Computer Graphics, and Audio Processing.