Travelling Salesman Problem using Dynamic Programming

Imagine you have to go to a party in another city and return back home as soon as possible. Which algorithm will you apply to reach your home so that you cover the shortest distance? Let us understand Travelling Salesman Problem in this guide.

What is Traveling Salesman Problem?

The Traveling Salesman Problem classic optimization problem in Computer Science. There is a salesman who wants to travel over a number of cities and he has to return back to the original city he started from and he has the choice to start from any of the cities he wants to. During his journey, we need to minimize the total distance traveled by him. 

Here is the main problem statement:

"We will be given a graph that will be represented in the form of an adjacency matrix, say distance, that denotes the distance between 2 cities, say, i and j. The distance[i][j] denotes the distance between 2 cities if the value of dist[i][j] == 0; this implies the given cities are not connected i.e. no direct edge exists between them. We can start from any node and we need to return to the original city through the shortest distance covering all the cities."

So, basically, we need to complete a cycle in this question, and such a cycle is known as the Hamiltonian cycle. A Hamiltonian cycle is a set of edges such that every node is visited only once and we come back to the original position. So in short, in this problem, we need to return a minimum weight Hamiltonian cycle. We just have to minimize the total cost of the cycle.

Let's first try to get a Hamiltonian cycle with minimum weight from the graph below. Given the following graph and the distance between cities he has traveled, let's find out the shortest path in which he can travel all the cities.

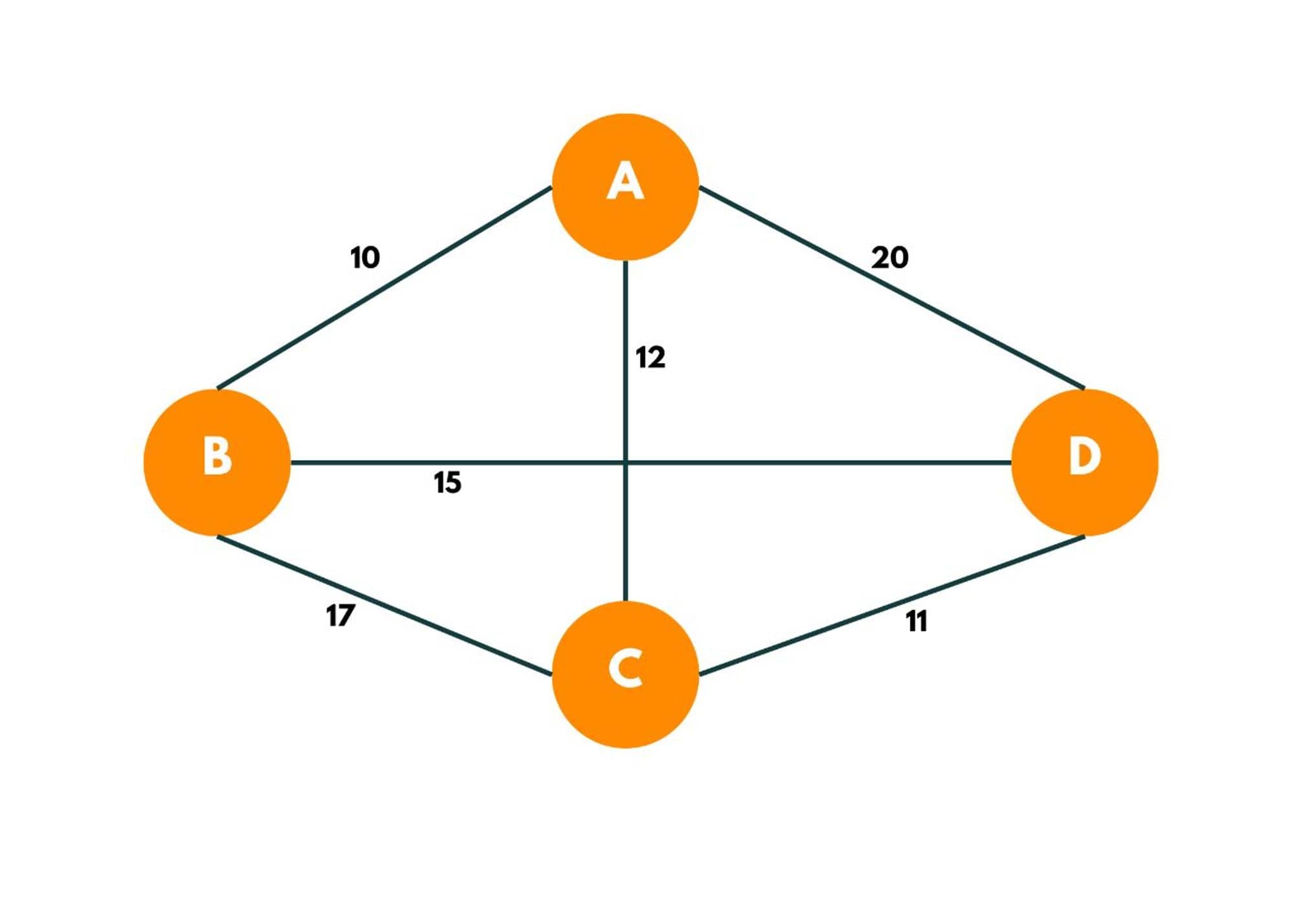
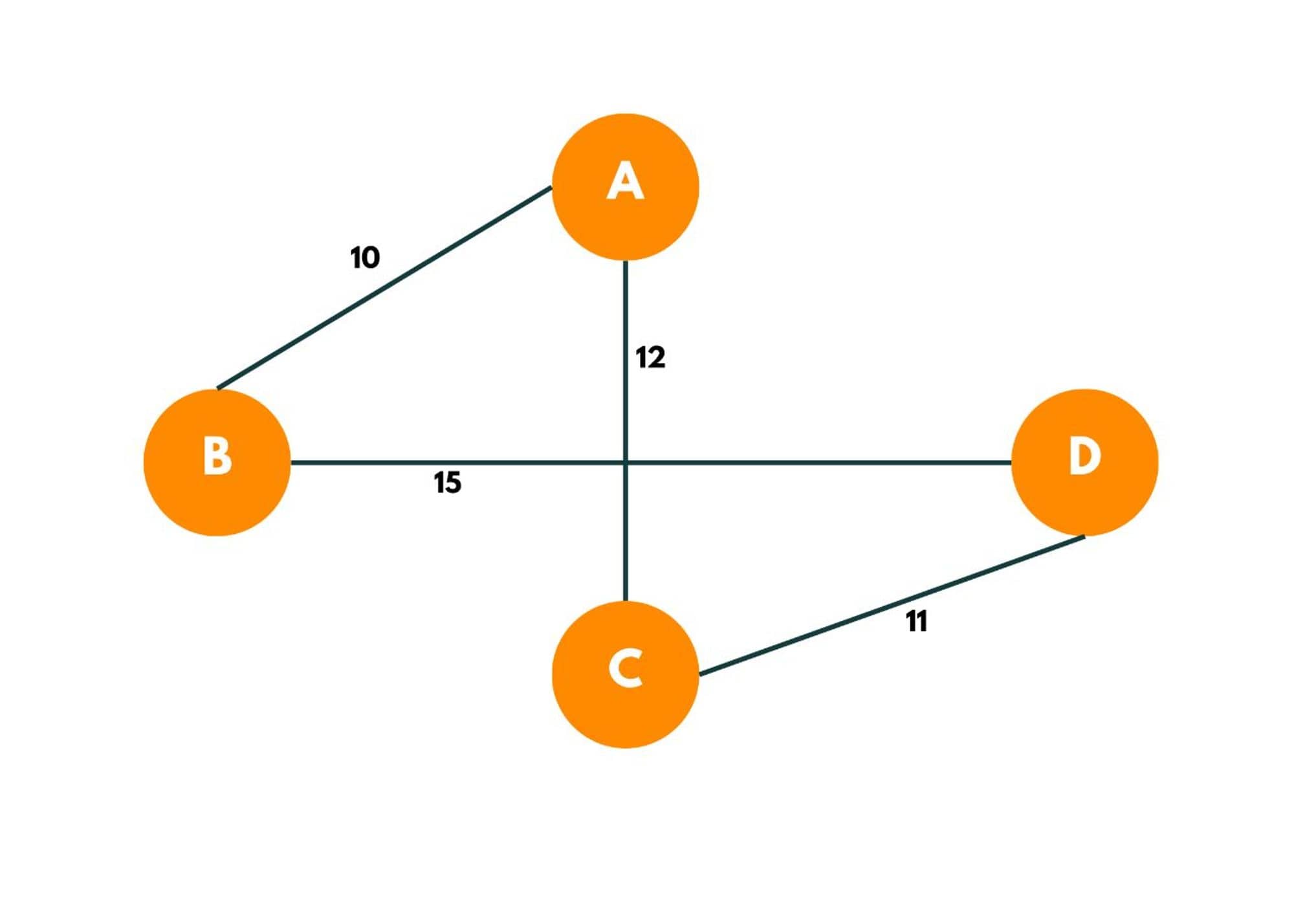
The Hamiltonian cycle with min weight can be:

How does the Algorithm Work?

Let's take an example of a graph say:

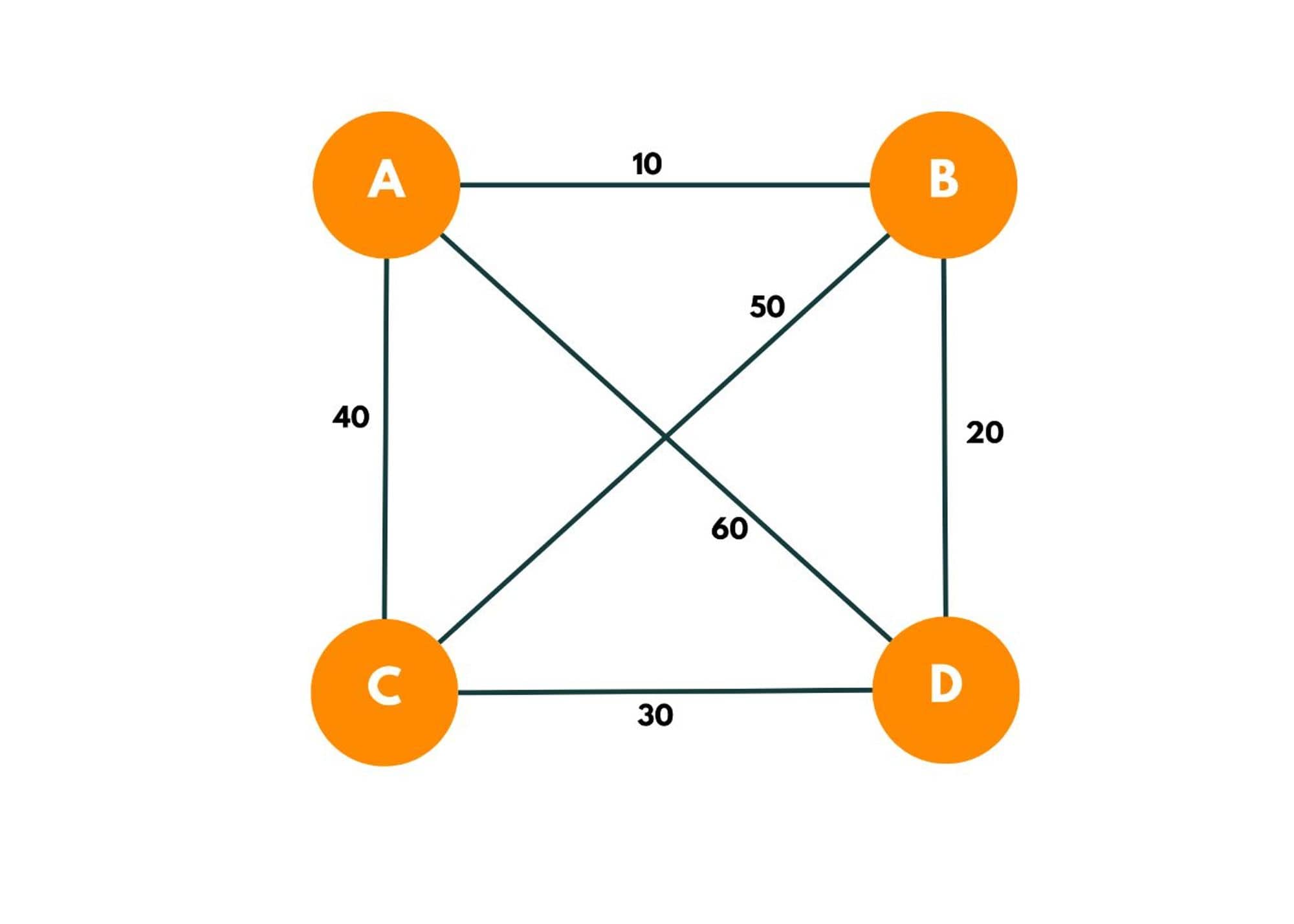
1. As we have an option to start from any position, we start from A.
2. Making a recursion tree and using bit masking. 

As 4 cities are there, the bit mask here would be = 0000 (at the beginning) respectively denoting D, C, B, and A  cities. The bit shows 0 for a particular city if it has not been visited and 1 if already been visited. So if bit mask = 1111 that means all bits are set, which implies all cities have been visited and we can denote this by 1<

We try to find the possible options that exist. This can be done by iterating over the adjacency matrix of A or the other way of doing so can be iterating over other cities and checking if they can be a possible option to travel from A. As we begin, we visit city A, and the bit mask value is now changed to 0001.

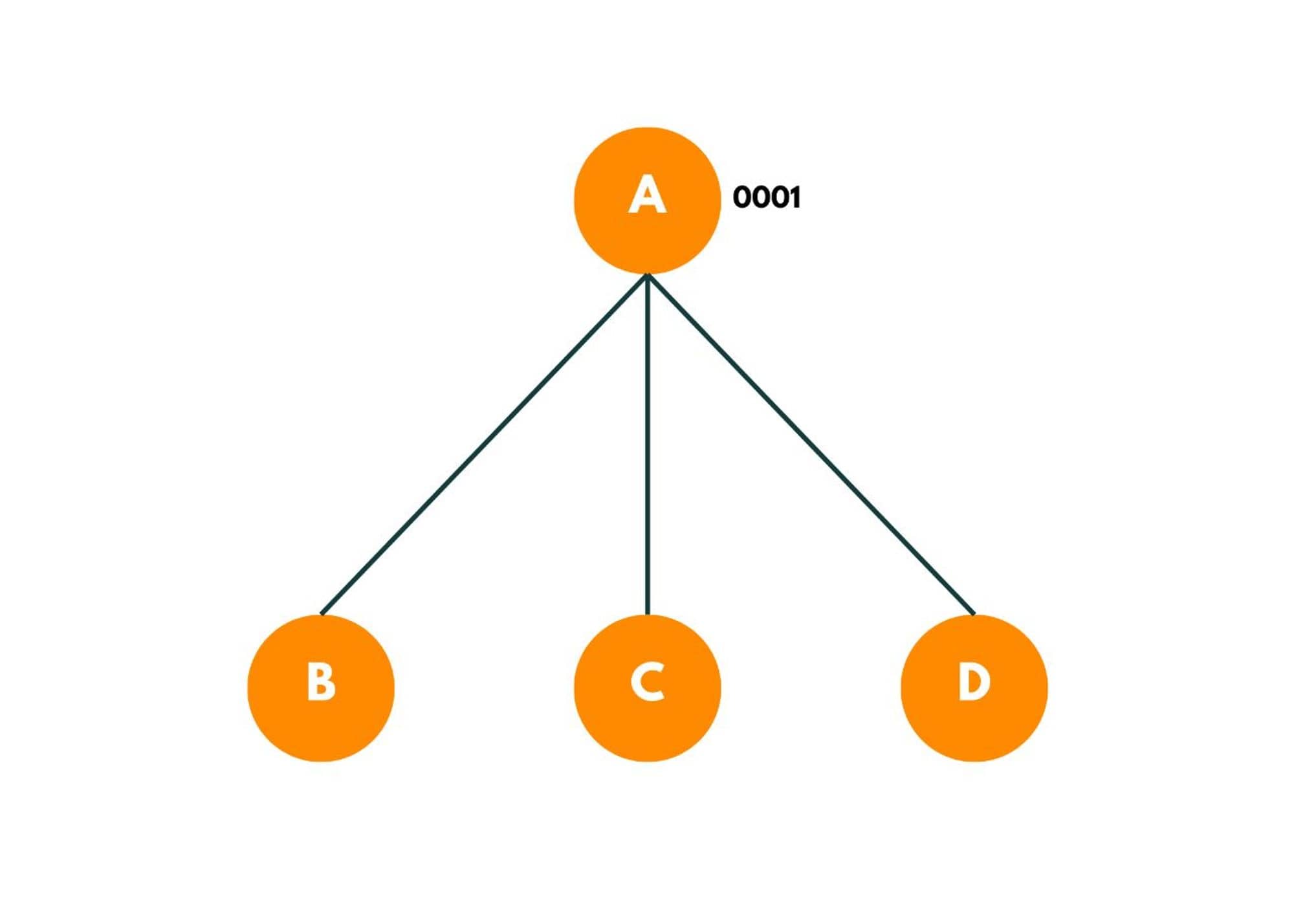
Each of these recursive branches denotes one path.

Now, as we move forward from A to B, we add the distance in a variable, say, ans. And we mark city B as visited.

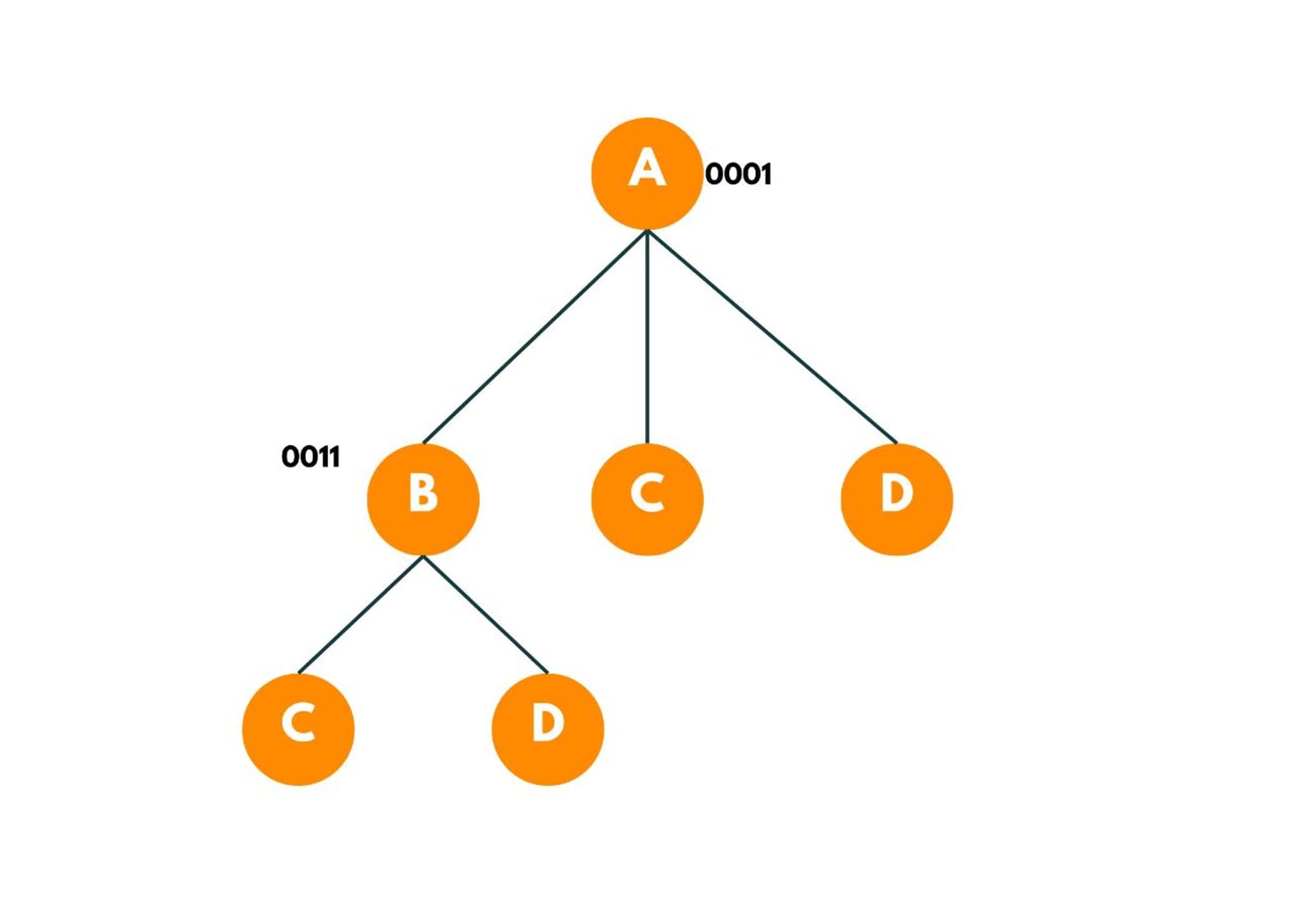
We add the distance to the answer. Now we only visit the cities from B that aren't visited yet so we have 2 options available C and D.

We then move to C and then to D while marking them visited and adding the cost to the and. Now here, we have explored each unvisited city. So now we backtrack, while marking each city as unvisited and go to the original city if a direct edge between them exists. As there is a direct edge from D to A and C to A, the nodes return the cost required to go back to the original source.

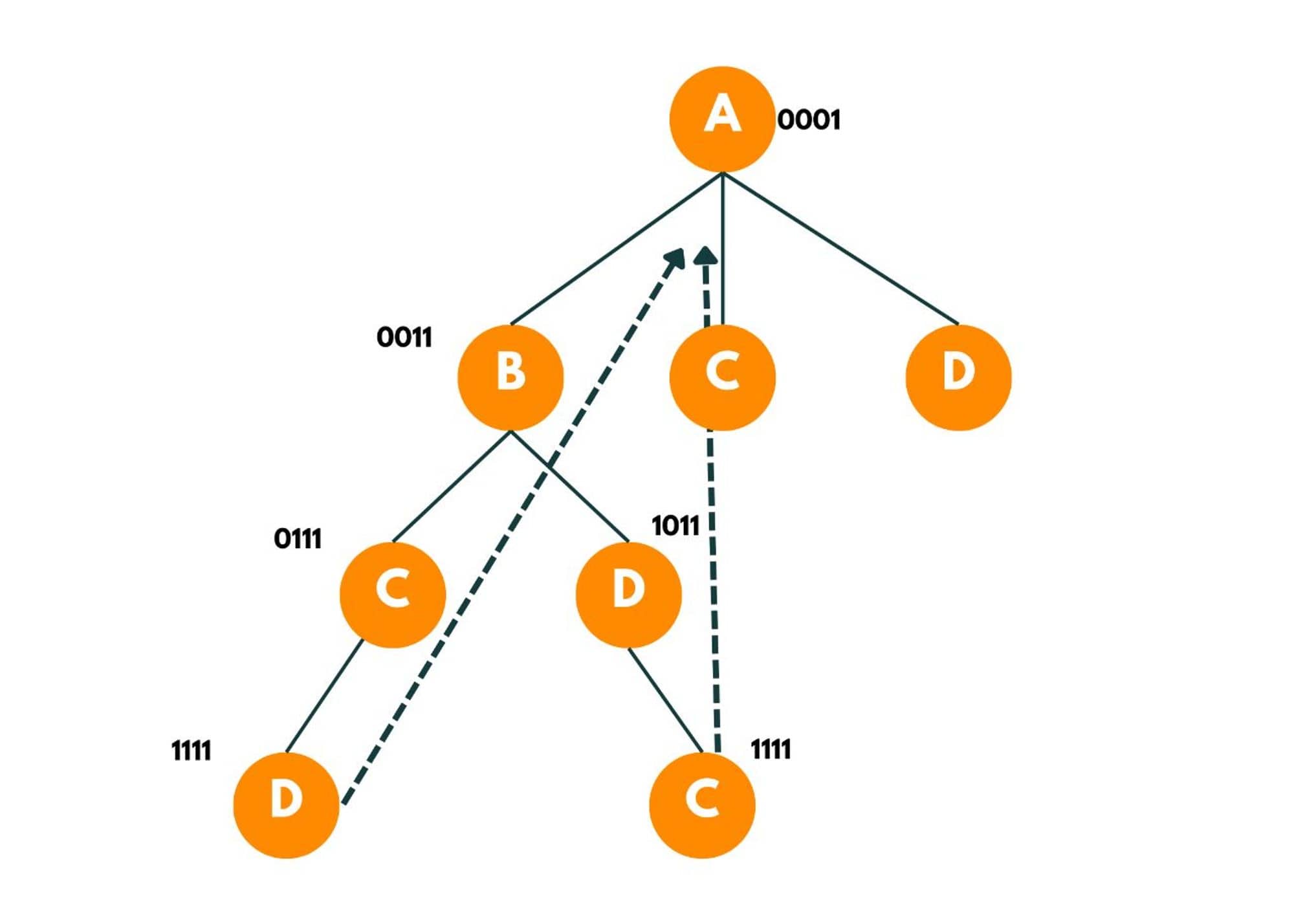
This way we explore each available option from the starting node. We also maintain a minimum cost variable that maintains the minimum cost spent to visit each city and return to the original city.

The recursion tree would look like this:

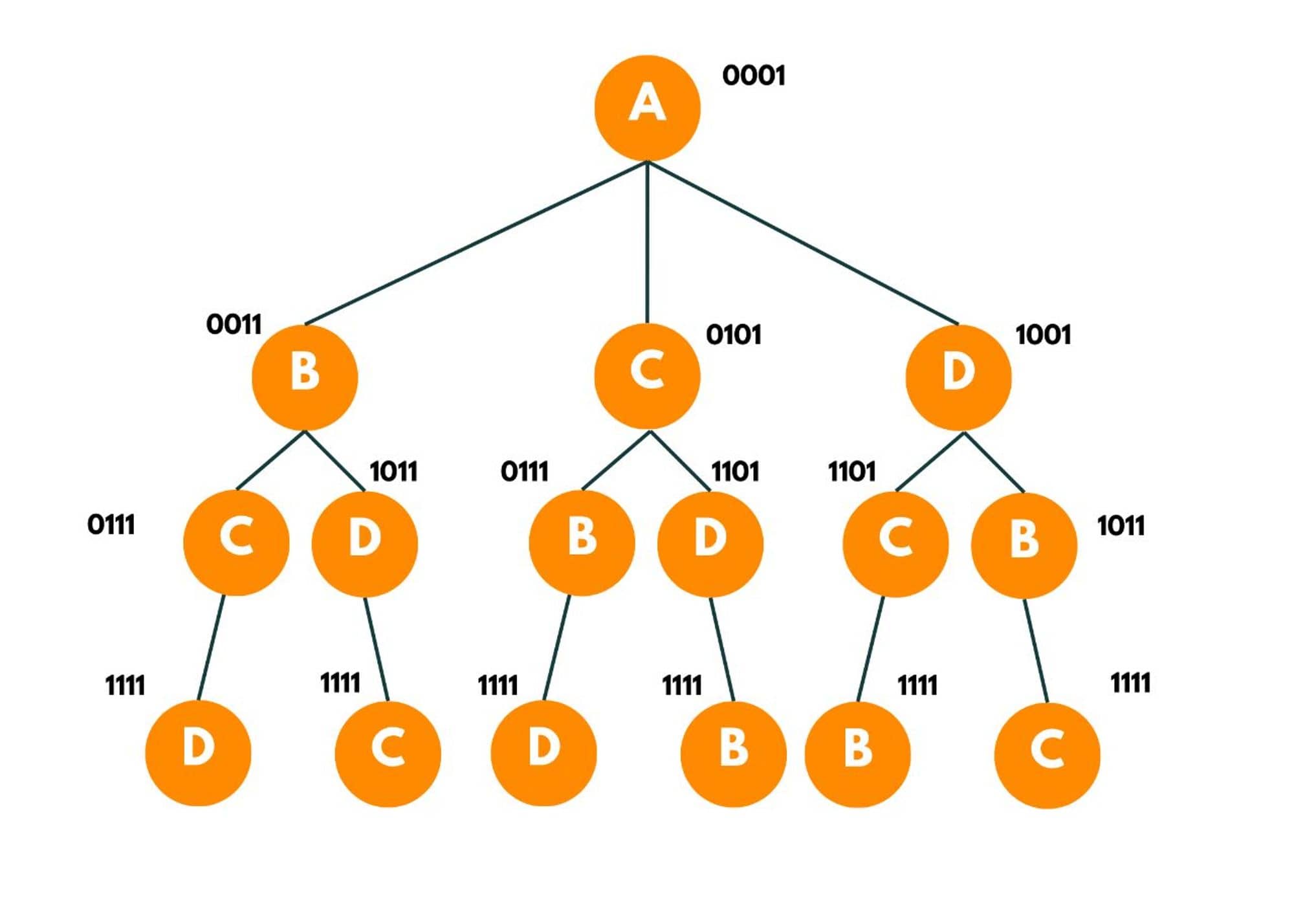
Traveling Salesman Algorithm

Here is the algorithm for Travelling Salesman Problem:

1. Define the mask as (1<<n)-1.
2. Create a function, say, tsp() having mask and city as arguments. As the mask denotes a set of cities visited so far, we iterate over the mask and get to know which city isn't visited.
3. The base case is when we visit all the cities i.e. mask has all of its bits set, we return the distance between the current city and the original city.
4. Then we try to visit the unvisited cities, we iterate over n cities and we check if the nth bit in the mask is 1 or 0.
   1. If the city is not visited, we make recursive calls by adding the distance of the original city and the city not visited and try to get the distance remaining from recursive calls
   2. In the recursive call, we pass a mask with the current city visited and the current city.

Travelling Salesman Problem in Java

Here is the complete Java Program to implement Travelling Salesman Problem:

import java.util.*;
public class TSP {
	
	public static void main(String[] args) {
		
		int ans = Integer.MAX_VALUE;
	
		int shortestDistance =  travellingSalesman(1, 0, ans);
		System.out.println("The shortest distance to visit all the cities is " + shortestDistance);
		
	}
	
	
	static int[][]distance = {{0, 20, 42, 25},{20, 0 , 30, 34}, {42, 30, 0, 10}, {25, 34, 10, 0}};
	static int n = 4;
	static int allCityVisited = (1<<n)-1;
	
	
	public static int travellingSalesman(int bitMask, int currCity, int ans) {
		
		if(bitMask == allCityVisited) {
			return distance[currCity][0];
		}
		
		// visiting the unvisited cities
		for(int city = 0; city < n; city++) {
			
			//checking if city has been visited or not, by checking ith bit in mask
			if((bitMask&(1<<city)) == 0) {
				// this means current city has not been visited
				//changing the city as visited
				bitMask = bitMask | (1<<city);
				
				//storing the distance of current city to the city and then fetching remaining distance from recursive call.
				int distAns = distance[currCity][city] + travellingSalesman(bitMask, city, ans);
				
				//storing the shortest distance
				ans = Math.min(ans,distAns);
			}
			
		}
		return ans;
	}
}

Output:

The shortest distance to visit all the cities is 50.

Time & Space Complexity 

Here we have fixed the source node as we get the same answer whether we start from A or B or any other node because of that cyclic permutation in this case.

The time complexity of the Travelling Salesman Problem comes out to be O(n-1!). The space complexity of this code comes out to be O(n).

Now we can notice that this bitmask can only have 2^n values ranging from 0000 to 1111. The city can take n values. So the total number of distinct states comes out to be (2^n )* n. Also in this approach, some sub-problems were getting overlapped.

To optimize this approach, we use DP. We will create a 2D DP table of the values and we memorize all the results for the given value of mask and city.

Optimized Approach using Dynamic Programming

Here is the simple way to implement the Optimized Approach using Dynamic Programming. Initially we make a 2D array of [2^n][n] and initially put -1 at each position as initially, all states have values = -1.

To avoid overlapping subproblems i.e. avoiding a state which has already been computed, we check dp[bitMask][city]. If this comes out to be -1, implies the city hasn't been visited, else the city has already been visited and we return dp[bitMask][city] = ans.

Here is the Java Code for Travelling Salesman Problem using Dynamic Programming:

import java.util.*;
public class TSP {
	
	public static void main(String[] args) {
		
		int ans = Integer.MAX_VALUE;
		int dp[][] = new int[16][4];
		
		for(int i = 0; i < (1<<n); i++) {
			for(int j = 0; j < n; j++) {
				dp[i][j] = -1;
			}
		}
		int shortestDistance =  travellingSalesman(1, 0, ans, dp);
		System.out.println("The shortest distance to visit all the cities is " + shortestDistance);
		
	}
	
	
	
	static int[][]distance = {{0, 20, 42, 25},{20, 0 , 30, 34}, {42, 30, 0, 10}, {25, 34, 10, 0}};
	static int n = 4;
	static int allCityVisited = (1<<n)-1;
	
	
	public static int travellingSalesman(int bitMask, int currCity, int ans, int[][] dp) {
		
		if(bitMask == allCityVisited) {
			return distance[currCity][0];
		}
		// if we arrive at a state which is already been computed
		if(dp[bitMask][currCity] != -1) {
			return dp[bitMask][currCity];
		}
		
		// visiting the unvisited cities
		for(int city = 0; city < n; city++) {
			
			//checking if city has been visited or not, by checking ith bit in mask
			if((bitMask&(1<<city)) == 0) {
				// this means current city has not been visited
				//changing the city as visited
				bitMask = bitMask | (1<<city);
				
				//storing the distance of current city to the city and then fetching remaining distance from recursive call.
				int distAns = distance[currCity][city] + travellingSalesman(bitMask, city, ans, dp);
				
				//storing the shortest distance
				ans = Math.min(ans,distAns);
			}
			
		}
		return dp[bitMask][currCity] = ans;
	}
}

Output:

The shortest distance to visit all the cities is 50.

The time complexity comes out to be O(n ^2 * (2*n)). As we are using an extra space of (2^n) *n. The space complexity comes out to be O((2^n) *n).

Conclusion 

Travelling Salesman is a classic problem demanding in-depth knowledge of graphs and DP. It is an NP-hard problem. The optimization used in this problem can be implemented in other questions of this type too. This problem is necessary from the interview point of view, so I hope you all understood it well!