Tree Traversal in Python (Inorder, Preorder & Postorder)

Trees are a complex topic for any programming beginner. In this article, we will study Tree Traversal in Python and the implementation of Inorder, Preorder, and Postorder tree traversal using recursion. It is one of the most important topics to solidify your knowledge of Data Structures.

What is Tree Traversal in Python?

Traversal is the process of traversing the node of the data structure. But if we use a data structure like the stack, queue, or linked list then it becomes difficult for traversing the nodes because this data structure is linear, and hence the time complexity of traversal increases.

Therefore, we use tree data structures (especially binary trees) when we have to perform the traversal process and find the elements easily. Using tree data structure, it becomes easy to traverse the nodes compared to other data structures because trees store the elements hierarchically, and hence, we can traverse the elements with their priority and path accordingly.

Tree traversing in Python refers to the process of visiting each node in a data structure like a tree. Traversal algorithms tell us the order in which the nodes of a tree are visited. 

Now, there are 3 main methods for Tree Traversal in Python with recursion using DFS which are:

1. In order Traversal (left, root, right)
2. Preorder Traversal (root, left, right)
3. Postorder Traversal (left, right, root)

The inorder traversal method is used for tree traversal to get the non-decreasing order of nodes. The preorder traversal method is used to get the prefix expression of an expression tree. Also, preorder traversal helps to create a copy of the tree. The postorder traversal method is used to get the postfix expression of an expression tree.

Remember that we will use the recursive function while traversing the tree and call the function again and again until we will traverse all the nodes of the tree.

Apart from this, we can also find the tree traversal without using the recursion method. The only difference between these two methods is that the tree traversal in Python without using the recursion process utilizes the stack data structure while traversal with recursion utilizes the array data structure.

Inorder Tree Traversal

Using the in-order traversal method, we first visit the left subtree of the original tree. Then we will traverse the root node of the tree and lastly the right subtree of the original tree. Here is the algorithm for Inorder Tree Traversal in Python:

1. Calling Inorder (left-subtree)
2. Visit the root node
3. Calling Inorder (right subtree)

Let us consider the following binary tree:

Now according to the inorder tree traversal method, we first traverse the left subtree of the original tree. Remember, even while traversing the left subtree, we will follow the same process i.e. left -> root -> right if the left child node of the original tree has furthermore child nodes. After traversing the left subtree, we will add the result to the array as shown below.

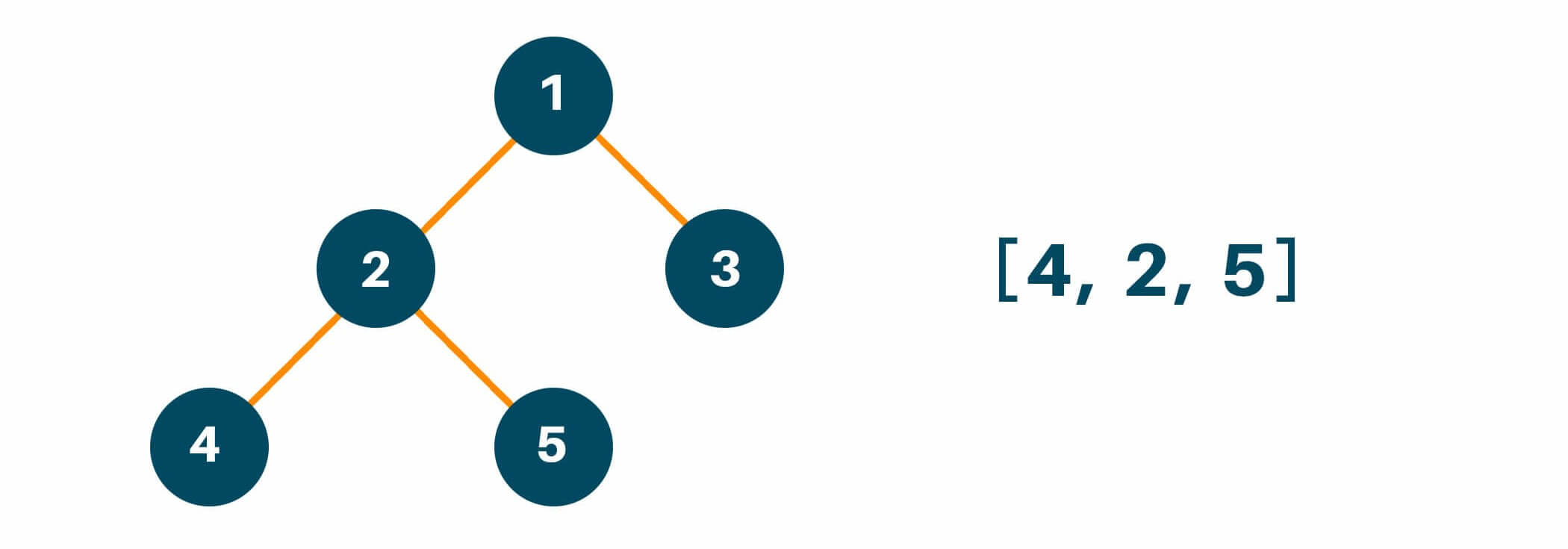
After following the first step, we will traverse the root node of the original tree as shown below.

Lastly, we will traverse the right subtree following the same process i.e. left -> root -> right if the right child node of the original tree has more than one child node.

Below is the Python code for Inorder Tree Traversal with recursion:

class TreeNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None 

def inorderTraversal(root):
    answer = []

    inorderTraversalUtil(root, answer)
    return answer

def inorderTraversalUtil(root, answer):

    if root is None:
        return

    inorderTraversalUtil(root.left, answer)
    answer.append(root.val)
    inorderTraversalUtil(root.right, answer)
    return

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(inorderTraversal(root))

Output:

[4, 2, 5, 1, 3]

Preorder Tree Traversal

Using the preorder traversal method, we first visit the root of the original tree. Then we will traverse the left subtree of the original tree and lastly the right subtree of the original tree. Below is the Python code for Preorder Tree Traversal with recursion:

1. Visit the root node
2. Calling preorder (left-subtree)
3. Calling preorder (right subtree)

Let us consider the following example tree:

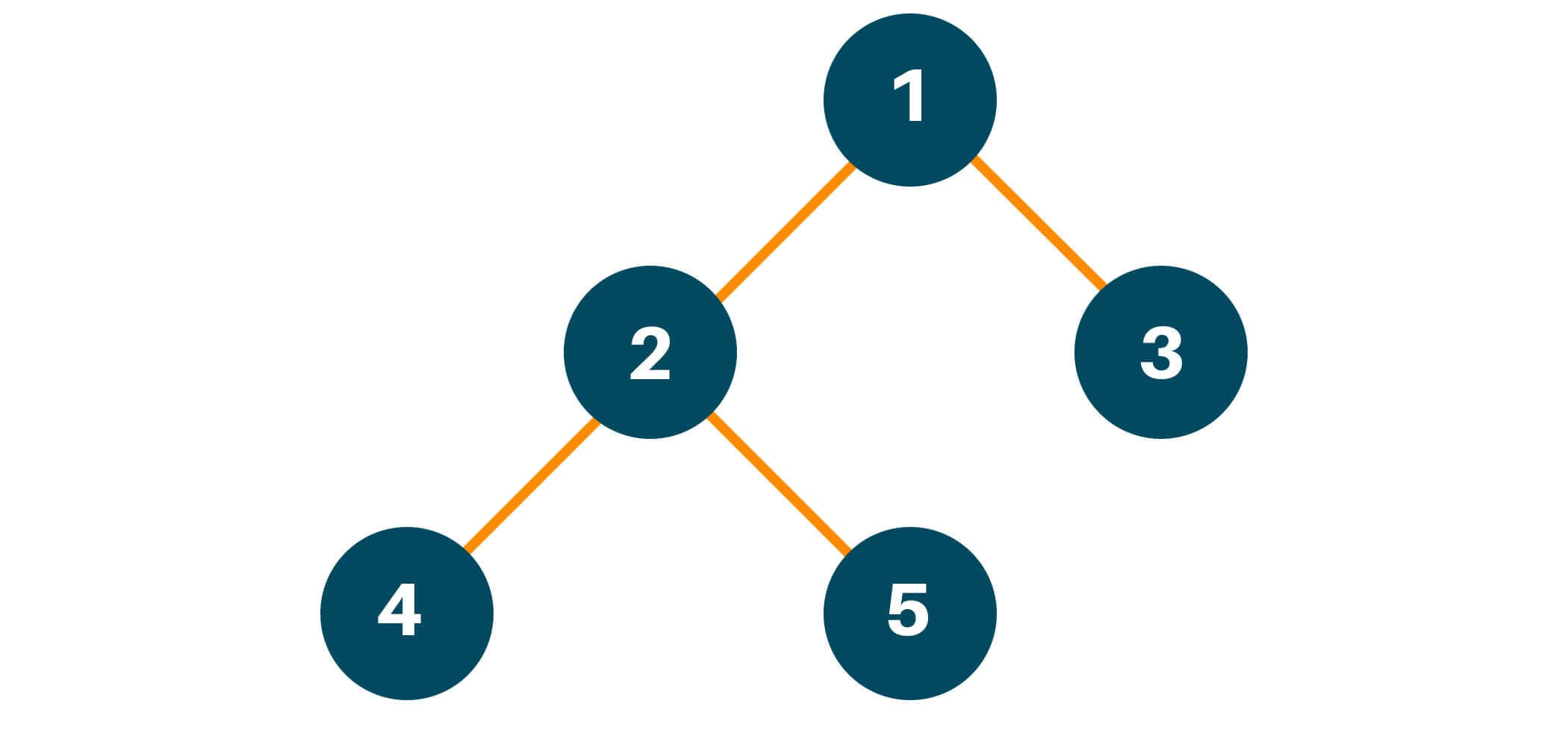
According to the preorder traversal method, we will first traverse the root node of the original tree and put it in the result array as shown in the figure below.

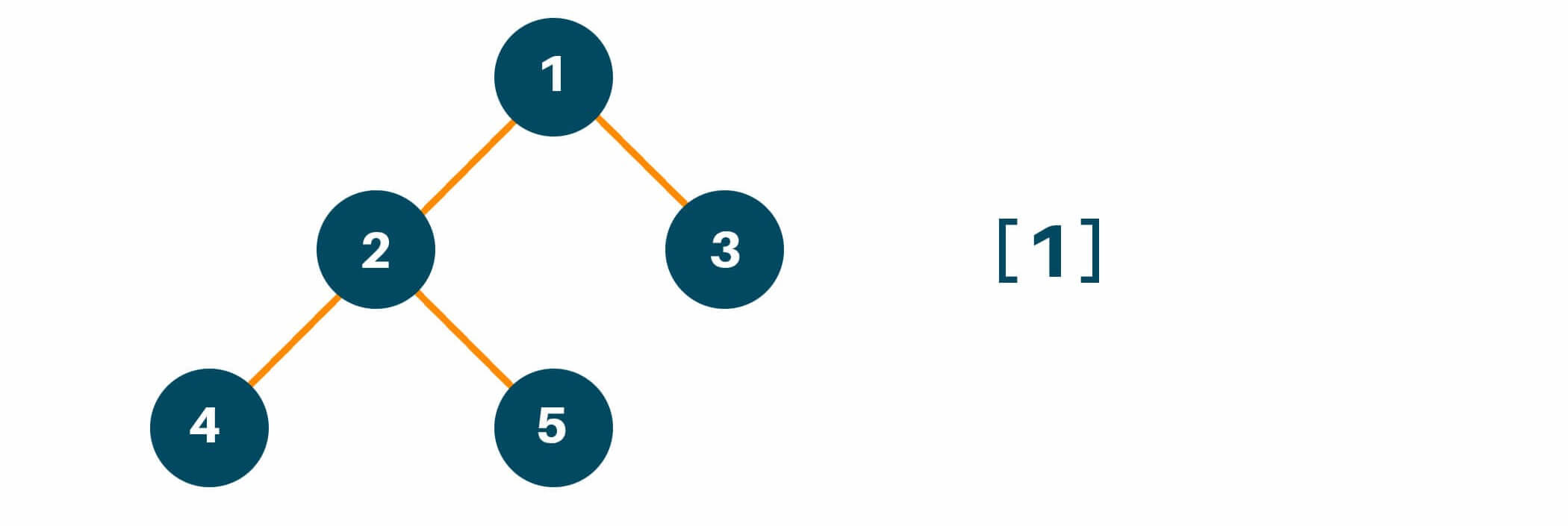
Then, we will traverse the left subtree of the original tree by calling the preorder traversal method. Here we will recursively call the function preorder to maintain the same process of traversal i.e root -> left -> right if the left child of the original tree has more than one child node and add the answer in the array as shown in the figure below.

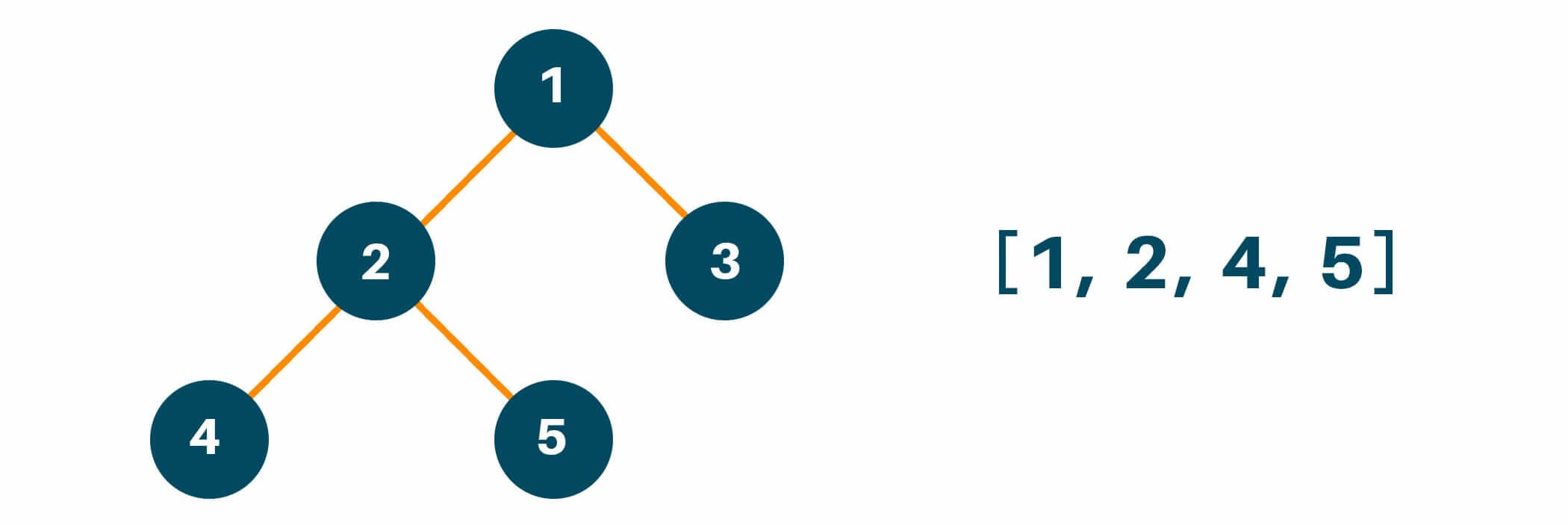
Lastly, we will traverse the right subtree of the original tree similarly like we did with the left subtree and put the result in the answer array as shown below.

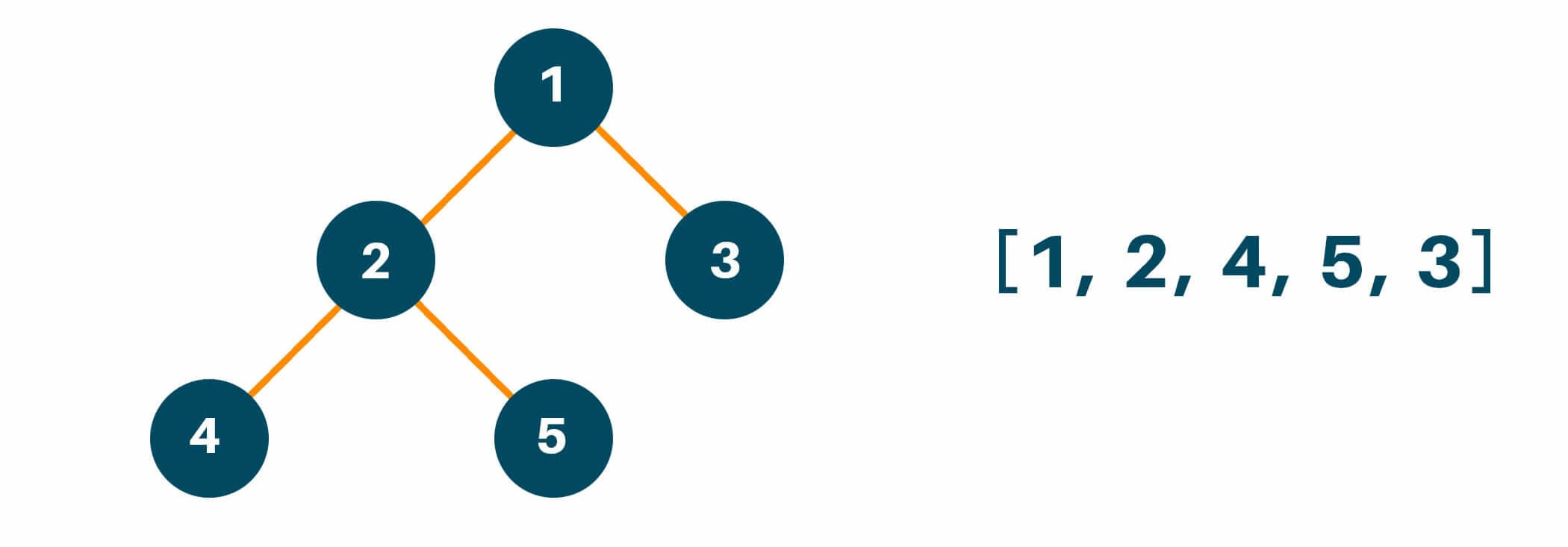
Below is the Python code of Preorder Tree Traversal with recursion:

class TreeNode:

    def __init__(self,val):
        self.val = val
        self.left = None
        self.right = None

def preorderTraversal(root):
    answer = []

    preorderTraversalUtil(root, answer)
    return answer

def preorderTraversalUtil(root, answer):

    if root is None:
        return 

    answer.append(root.val)

    preorderTraversalUtil(root.left, answer)

    preorderTraversalUtil(root.right, answer)

    return

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(preorderTraversal(root))

Output:

[1, 2, 4, 5, 3]

Postorder Tree Traversal

Using the postorder tree traversal method we first visit the left subtree of the original tree followed by the right subtree and lastly the root node of the original tree. Below is the Python code for Postorder Tree Traversal with recursion:

1. Calling left-subtree
2. Calling right-subtree
3. Visit root node

Let us consider the following example tree:

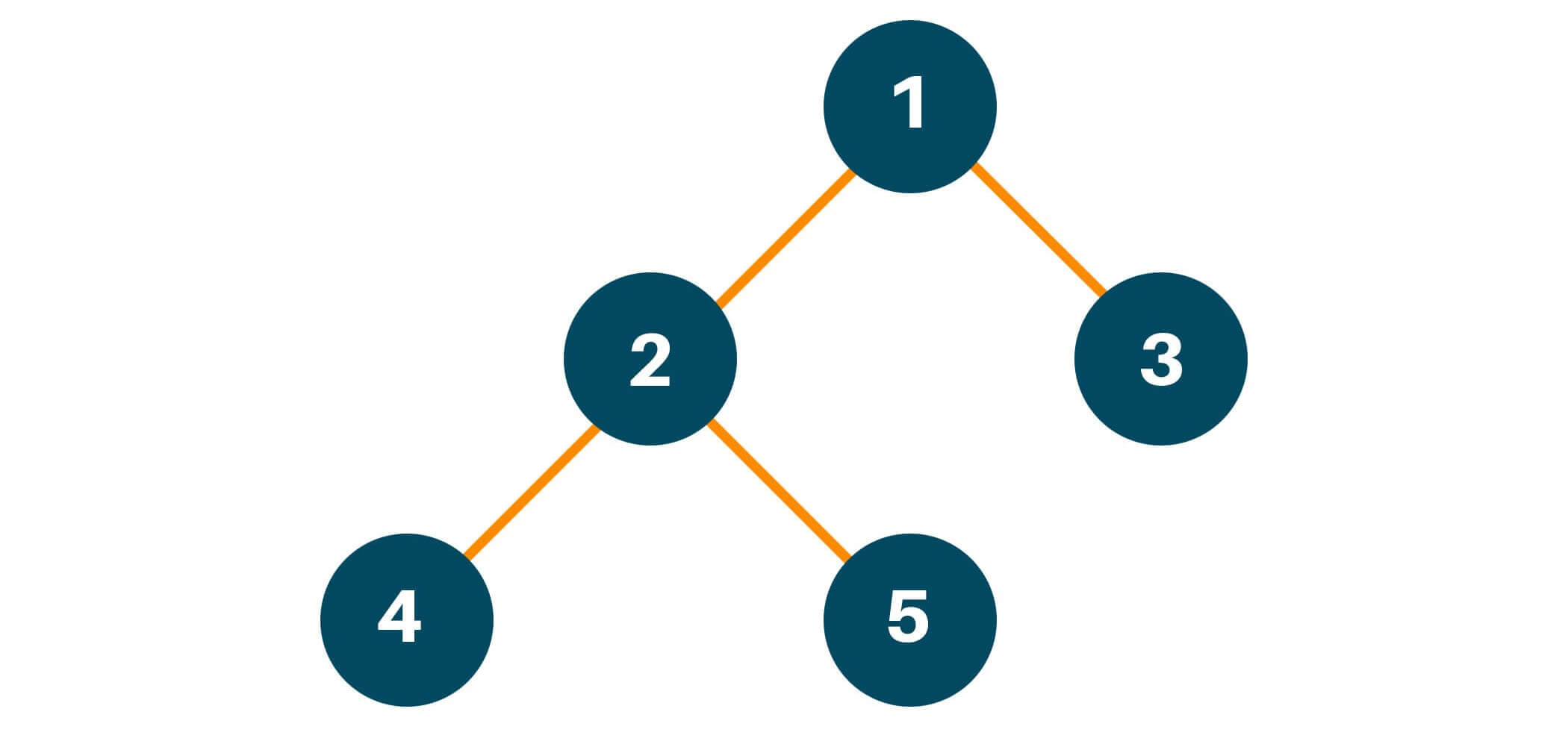
Using the postorder traversal method, we will first traverse the left subtree of the original tree. Remember that we will follow the same process of traversing of left subtree i.e left -> right -> root if the left subtree has more than one child node and then put the result in the answer array as shown in the figure.

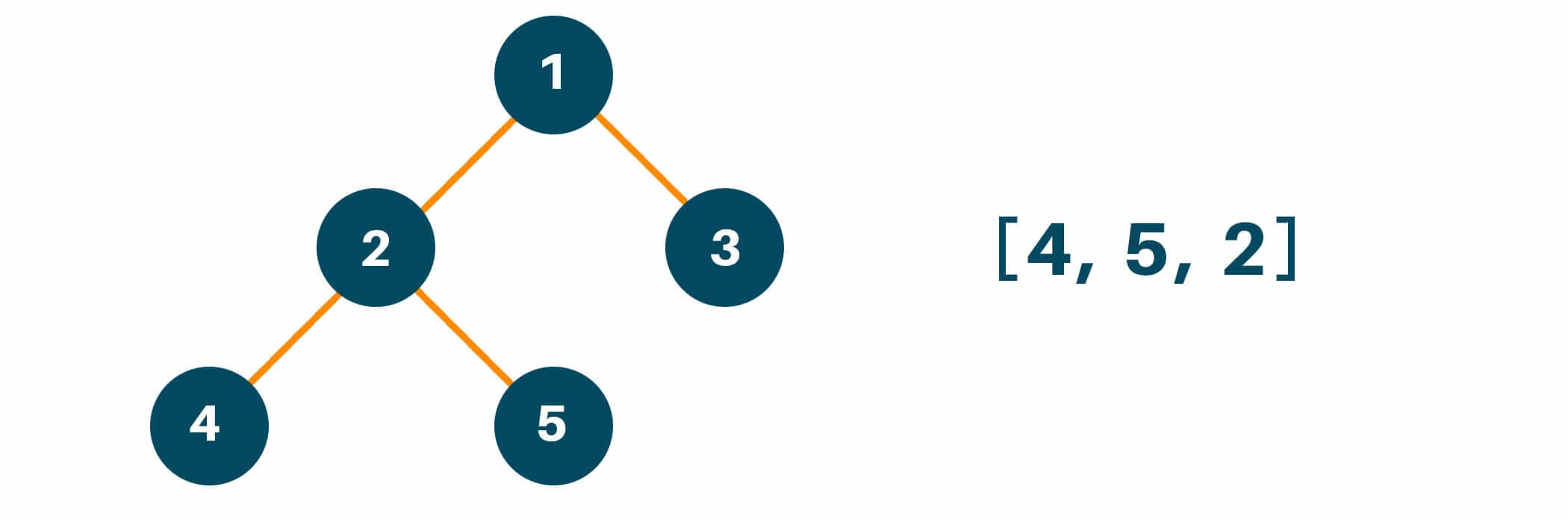
Later we will traverse the right subtree of the original tree similarly like we did with the left subtree and add the answer in the result array as shown below.

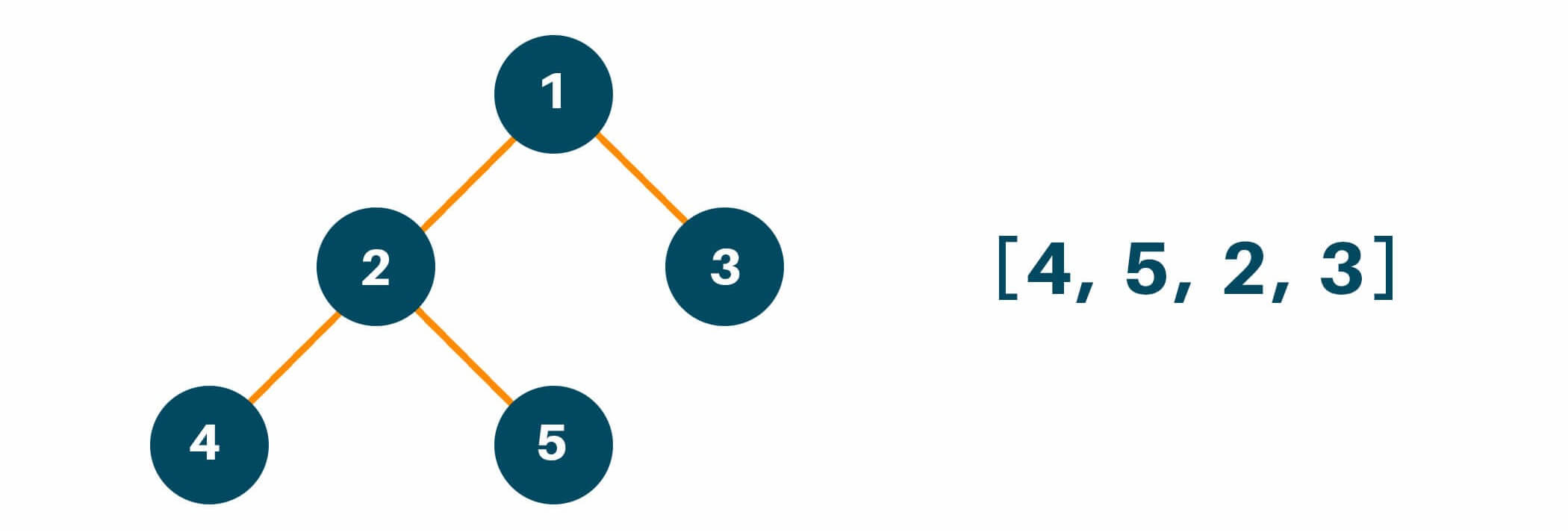
And lastly, we will traverse the root node of the original tree and finish our traversal method as shown in the figure below.

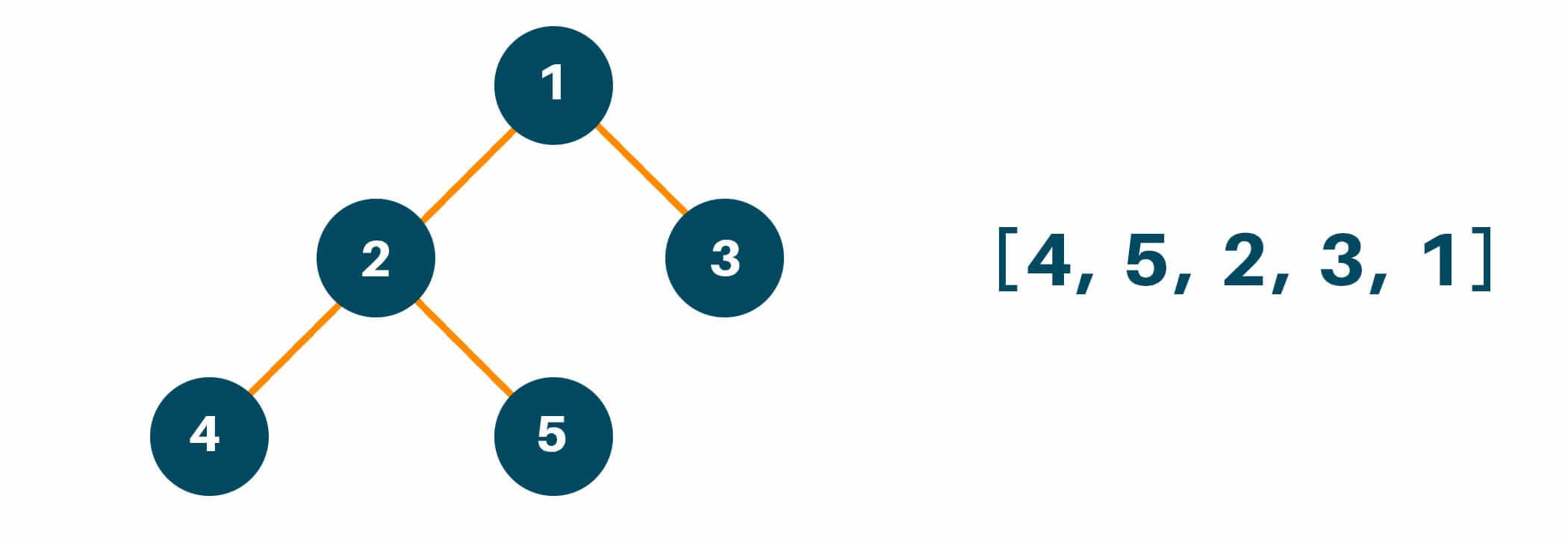
Below is the Python code for Postorder Tree Traversal with recursion:

class TreeNode:

    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def postorderTraversal(root):
    answer = []

    postorderTraversalUtil(root, answer)
    return answer

def postorderTraversalUtil(root, answer):

    if root is None:
        return

    postorderTraversalUtil(root.left, answer)

    postorderTraversalUtil(root.right, answer)

    answer.append(root.val)

    return

root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print(postorderTraversal(root))

Output:

[4, 5, 2, 3, 1]

Time Complexity

In tree traversal in Python using recursion, the time complexity is O(n) where there are n nodes in the tree. While the space complexity is also O(n) for n nodes present in an answer array.

Python Traverse Tree without Recursion

The act of precisely viewing each node in a tree data structure once is known as tree traversal. The two major methods for moving through a tree are breadth-first traversal and depth-first traversal. While breadth-first traversal is frequently performed iteratively, depth-first traversal can be performed recursively or sequentially. 

What are the 2 Types of Tree Traversal?

Let's quickly examine the depth-first and breadth-first approaches to tree traversal before moving on to breadth-first traversal.

• Depth-First Traversal: Beginning at the root of a tree and proceeding as far down as feasible before turning around is known as a "depth-first traversal," which requires stopping at every node along the way. Pre-order traversal, in-order traversal, and post-order traversal are the three most popular techniques for depth-first navigation. We visit the current node, the left subtree, and the right subtree in the pre-order traversal. We visit the left subtree, the current node, and the right subtree in an in-order traversal. The left subtree, followed by the right subtree, and finally the present node are all visited during post-order traversal. You can do depth-first traversal iteratively or recursively. Although it is typically easier to build, recursive traversal can be less effective for very deep trees.
• Breadth-First Traversal: In a breadth-first traversal, each node in a tree is visited one level at a time, working down from the root. Before going to the next level, we visit every node at the previous level. A queue is frequently used to keep track of the nodes we need to visit during breadth-first traversal. The root node is first added to the queue, after which the next node in the queue is repeatedly dequeued, visited, and re-enqueued with its children. This procedure is carried out until the queue is empty.

Using a queue data structure, we can construct breadth-first traversal in Python. Here is an illustration of how to utilize a deque from the collections module in code:

from collections import deque

def breadth_first_traversal(root):
    queue = deque()
    queue.append(root)

    while queue:
        node = queue.popleft()
        visit(node)

        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

At the beginning of this code, we create an empty deque as well as add the root node to it. The loop continues as long as the deque is not empty after that. We dequeue the next node from the deque, visit it, and then enqueue its offspring if they are present in each iteration of the loop.

Any function that accepts a node as an argument and performs some action on it, such as displaying its value or adding it to a list, might be considered a visit function.

Conclusion

Overall, we learned about the theory and the applications of Tree Traversal in Python using recursion and its methods of traversing with recursive nature. Happy Learning :)