Suppose there is a museum with many hallways and turns. It displays very valuable collectibles and you want to keep them safe. The plan is to install surveillance cameras in every hallway so the cameras can see every collectible. How would you do it efficiently so that the minimum number of cameras is required? This is exactly where Vertex Cover Problem comes into play.
What is the Vertex Cover Problem?
The Vertex Cover Problem involves finding the smallest set of vertices in a given graph such that every edge of the graph is incident to at least one vertex in that set. It is a well-known computational problem in graph theory,
More formally, given an undirected graph G(V, E), a vertex cover is a subset of vertices V' such that every edge in E has at least one of its endpoints in V'. The goal is to find the smallest possible vertex cover.
It has many real-world applications in network design, transportation, and resource allocation. Its ability to identify the minimum set of elements required to cover all edges in a graph makes it an important problem to solve in many different contexts.
Vertex Cover Problem Example
Here's an example of the vertex cover problem:
Consider the following undirected graph:
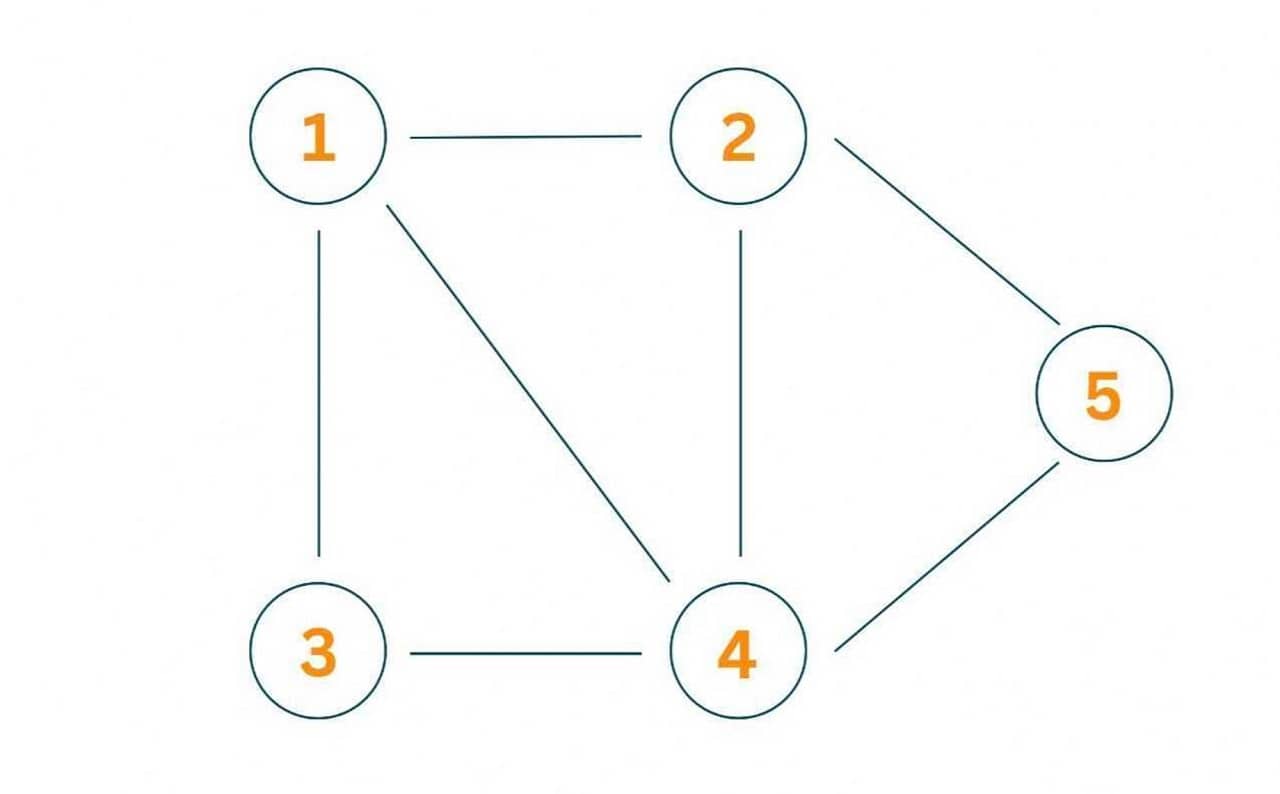
A possible vertex cover for this graph is {1, 4, 5} since these three vertices cover all the edges in the graph.
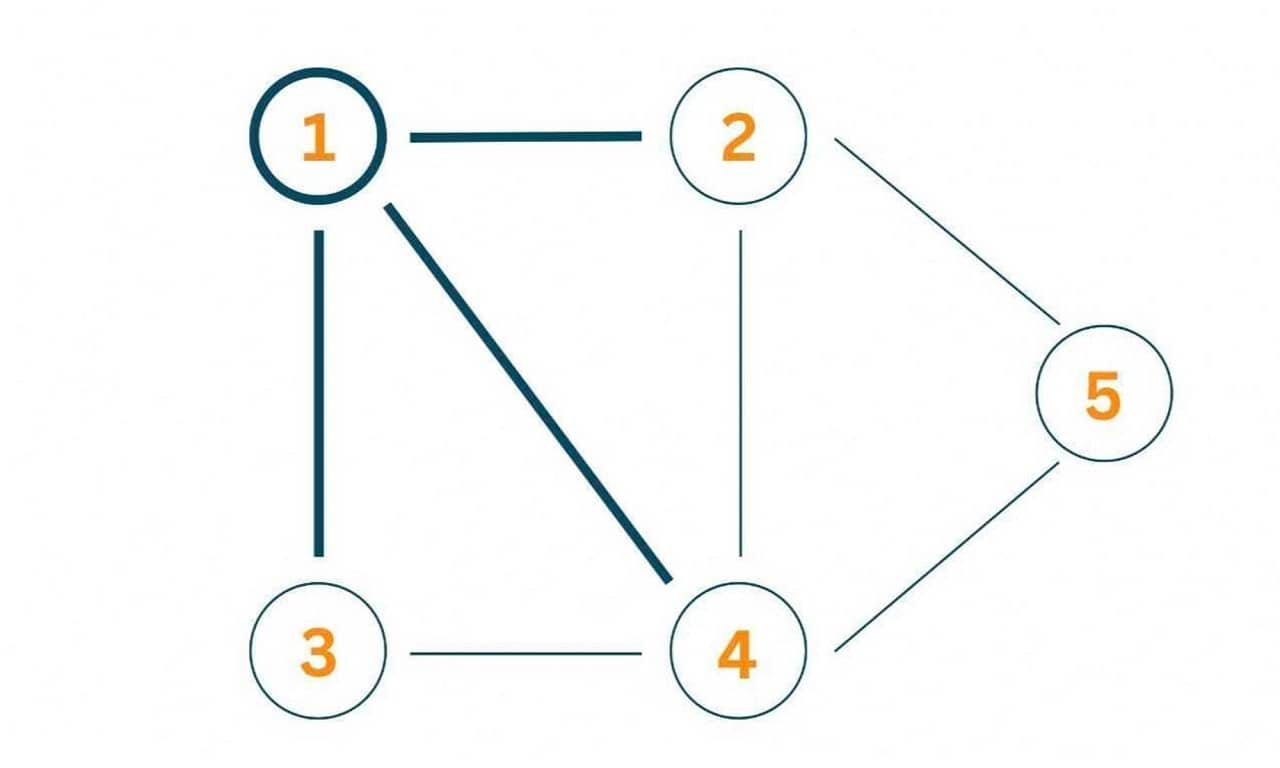
Specifically, vertex 1 covers the edge between 1 and 2, between 1 and 4, and between 1 and 3.
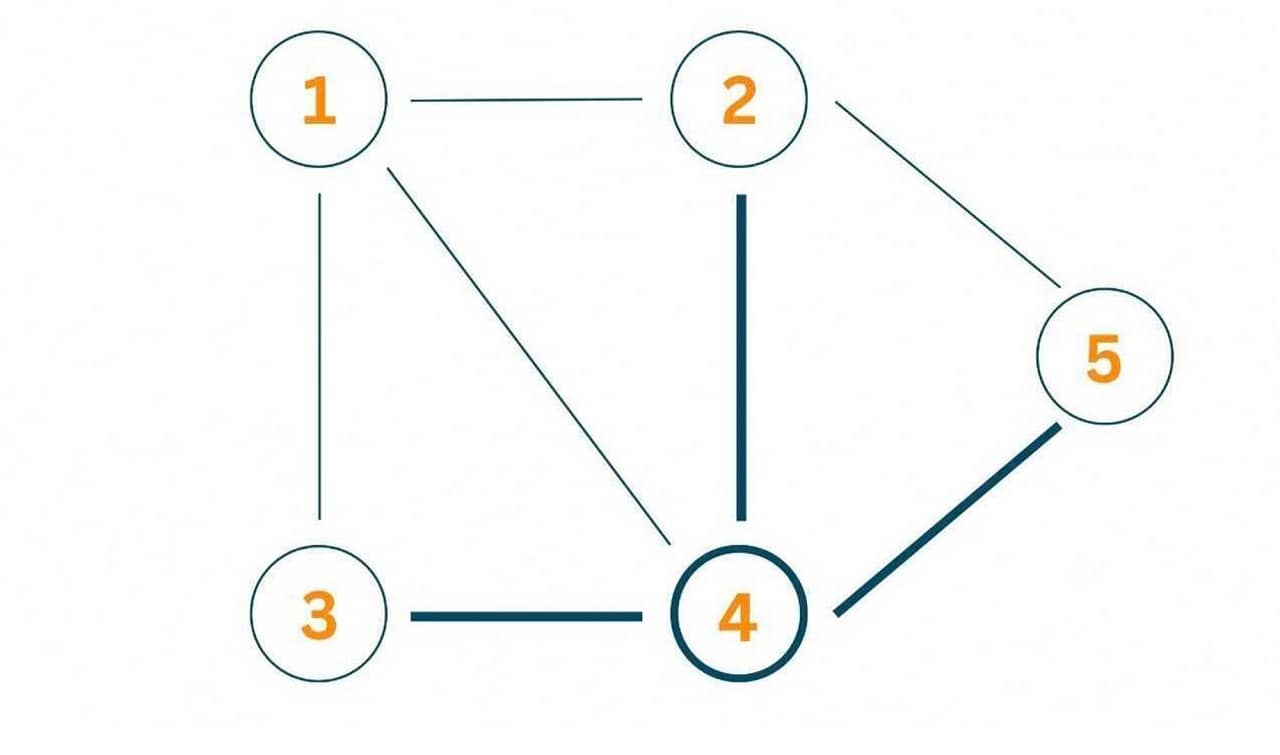
Vertex 4 covers the edges between 4 and 5, between 4 and 3, and between 4 and 2.
Vertex 5 covers the edge between 5 and 2.
Note that there are other possible vertex covers for this graph, such as {2, 3, 4}, {1, 2, 3, 4}, {1, 2, 4, 5}, etc. However, the smallest vertex cover is {1, 4, 5} and {2,3,4}, which contain only three vertices.
Vertex Cover Problem Algorithm
There are several algorithms to solve the Vertex Cover Problem. Here are two common algorithms:
Greedy Algorithm
The greedy algorithm for the Vertex Cover Problem is a simple heuristic that can provide a good approximation to the optimal solution. The algorithm starts with an empty vertex cover set and iteratively adds vertices to the set until all edges in the graph are covered.
The basic idea behind the greedy algorithm is to choose the vertex that covers the maximum number of uncovered edges in each iteration. The algorithm iteratively selects an arbitrary edge from the set of uncovered edges and adds both endpoints of the edge to the vertex cover set.
Then, it removes all edges incident on either endpoint of the selected edge from the set of uncovered edges. The algorithm repeats this process until all edges are covered.
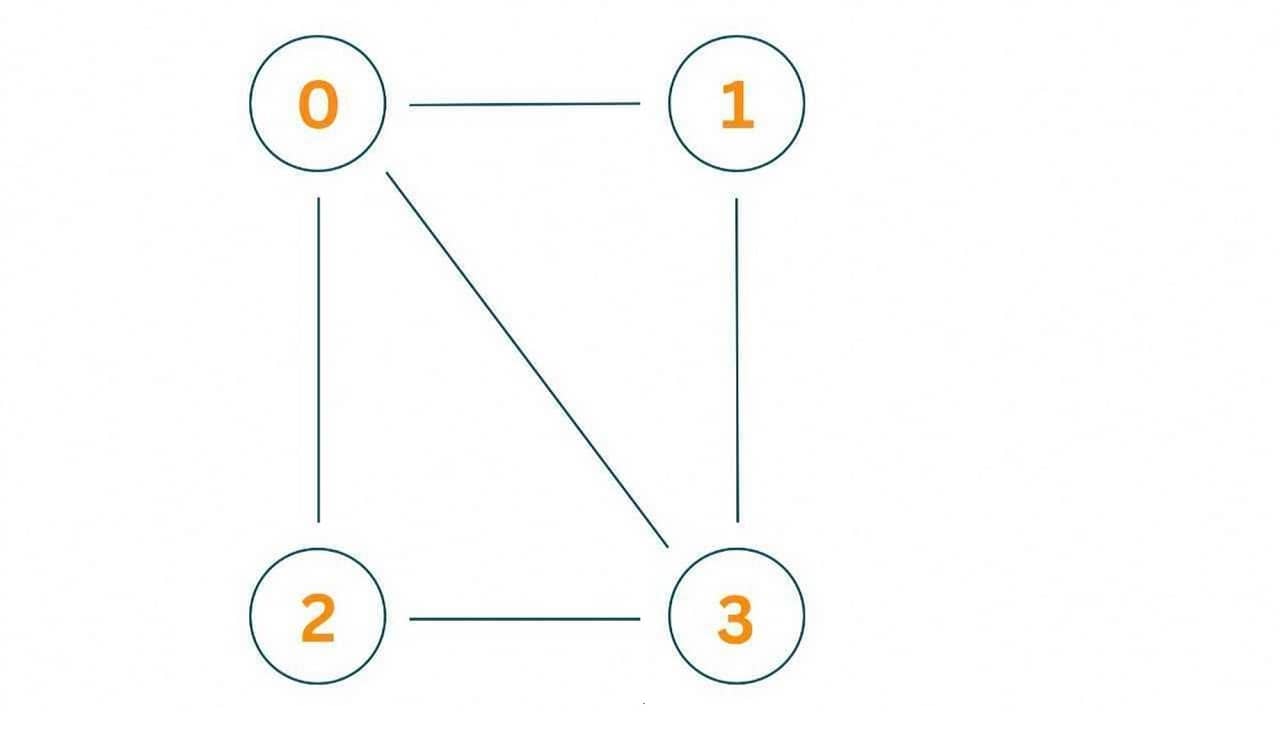
Here is a step-by-step example of the greedy algorithm. Let's consider a simpler graph with 4 vertices:
- Initialize an empty vertex cover set, V' = {}.
- Select an arbitrary edge, say (1,2), from the set of uncovered edges.
- Add both endpoints of the edge, 1 and 2, to the vertex cover set: V' = {1,2}.
- Remove all edges incident on 1 or 2 from the set of uncovered edges: {(3,1), (2,4)}.
- Repeat steps 2-4 until all edges are covered.
- Select edge (3,4), which is the only remaining uncovered edge.
- Add both endpoints of the edge, 3 and 4, to the vertex cover set: V' = {1,2,3,4}.
- The vertex cover set V'={1,2,3,4} covers all edges in the graph.
The greedy algorithm has a time complexity of O(E*log(V)), where E is the number of edges and V is the number of vertices in the graph. However, it may not always provide the optimal solution, and its performance depends on the structure of the graph
Approximation Algorithm
The approximation algorithm for the Vertex Cover Problem is another method for finding a good solution to the problem, but with a performance guarantee. This approach ensures that the size of the discovered vertex cover is no larger than twice that of the ideal vertex cover.
The algorithm starts by finding a maximum matching in the graph. An edge set is said to be "matching" if no two of its edges have the same vertex. A matching with the most edges is said to be a maximum matching. Then, the algorithm adds all vertices that are incident to the edges in the matching to the vertex cover set. Finally, it returns the resulting vertex cover.
Here is a step-by-step example of the approximation algorithm. Let's consider the same above graph:
- Find a maximum matching in the graph. In this case, the maximum matching is {(1,2), (3,4)}.
- Add all vertices that are incident to the edges in the matching to the vertex cover set. In this case, the vertices 1, 2, 3, and 4 are all incident to the edges in the matching.
- The resulting vertex cover set is V'={1,2,3,4}, which covers all edges in the graph.
- The time complexity of the approximation algorithm is O(E), where E is the number of edges in the graph. Note that the size of the resulting vertex cover may not be optimal, but it is guaranteed to be at most twice the size of the optimal vertex cover.
The approximation algorithm is useful in situations where finding the optimal solution is computationally expensive or not practical. It provides a fast and simple method for finding a good solution to the Vertex Cover Problem with a performance guarantee.
Vertex Cover Problem in C++
Now that we covered the basics with an example and algorithm, it's time to code the solution. Let's write a code for the following graph:
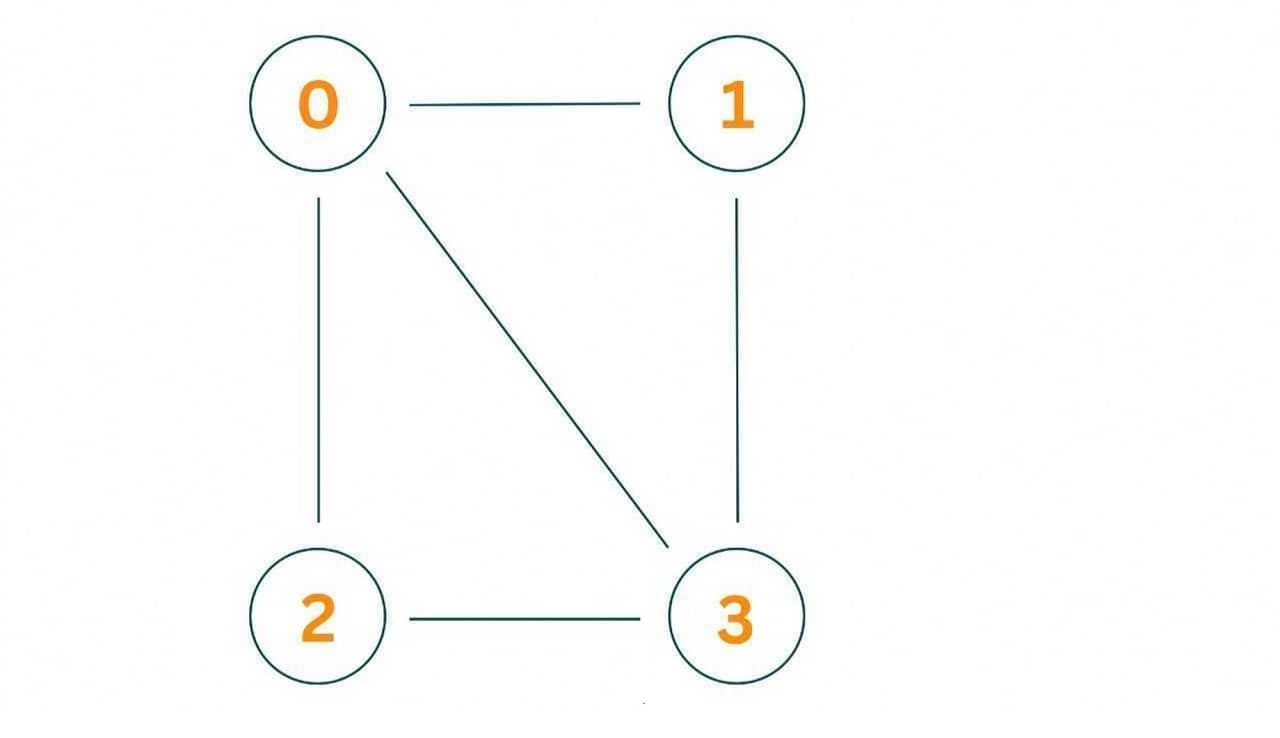
The following is the C++ program for Vertex Cover Problem for this graph:
#include #include #include using namespace std; // Graph representation using adjacency list class Graph { public: int V; vector<vector<int>> adjList; Graph(int V) { this->V = V; adjList.resize(V); } void addEdge(int u, int v) { adjList[u].push_back(v); adjList[v].push_back(u); } }; // Greedy algorithm for Vertex Cover Problem unordered_set<int> vertexCover(Graph& graph) { unordered_set<int> cover; // Initialize the set of uncovered edges vector<bool> visited(graph.V, false); for (int u = 0; u < graph.V; u++) { for (int v : graph.adjList[u]) { if (!visited[u] && !visited[v]) { cover.insert(u); cover.insert(v); visited[u] = visited[v] = true; } } } return cover; } // Driver code int main() { Graph graph(4); graph.addEdge(0, 1); graph.addEdge(1, 2); graph.addEdge(2, 3); unordered_set<int> cover = vertexCover(graph); cout << "Vertex cover: "; for (int v : cover) { cout << v << " "; } cout << endl; return 0; }
Output:
Vertex cover: 3 2 1 0
Vertex Cover Problem in Python
The below code is the Python implementation of the Vertex Cover Problem::
from typing import List, Set from collections import defaultdict # Graph representation using adjacency list class Graph: def __init__(self, V: int): self.V = V self.adjList = defaultdict(list) def addEdge(self, u: int, v: int): self.adjList[u].append(v) self.adjList[v].append(u) # Greedy algorithm for Vertex Cover Problem def vertexCover(graph: Graph) -> Set[int]: cover = set() # Initialize the set of uncovered edges visited = [False] * graph.V for u in range(graph.V): for v in graph.adjList[u]: if not visited[u] and not visited[v]: cover.add(u) cover.add(v) visited[u] = visited[v] = True return cover # Driver code if __name__ == '__main__': graph = Graph(4) graph.addEdge(0, 1) graph.addEdge(1, 2) graph.addEdge(2, 3) cover = vertexCover(graph) print('Vertex cover:', cover)
Output:
Vertex cover: {0, 1, 2, 3}
The algorithms mentioned above have an O(V + E) time complexity, where V is the number of graph vertices and E is the number of edges.
These approaches have an O(V) space complexity, where V is the number of graph vertices. This is so that we can store the visited vertices in an array of size V.
Time Complexity
The time complexity of the Vertex Cover Problem is exponential, which means it grows very quickly as the size of the input graph increases.
In particular, the best-known exact algorithm for solving the Vertex Cover Problem has a time complexity of O(1.2738^n), where n is the number of vertices in the graph. This algorithm is based on the so-called "iterative compression" technique and is not practical for graphs with more than about 50 vertices.
Conclusion
We covered everything about Vertex Cover Problem with how to code in C++ and Python. By the way, In the case of our museum example, all the hallways are edges, and places, where the camera can be installed, are the vertices.