Traversing a binary tree means visiting all the nodes of the tree in a specific order. There are several ways to traverse a binary tree, such as in-order traversal, pre-order traversal, and post-order traversal. In this article, we will focus on the zig-zag traversal of a binary tree and learn about the various approaches to solving it.
Zig-Zag Traversal of Binary Tree
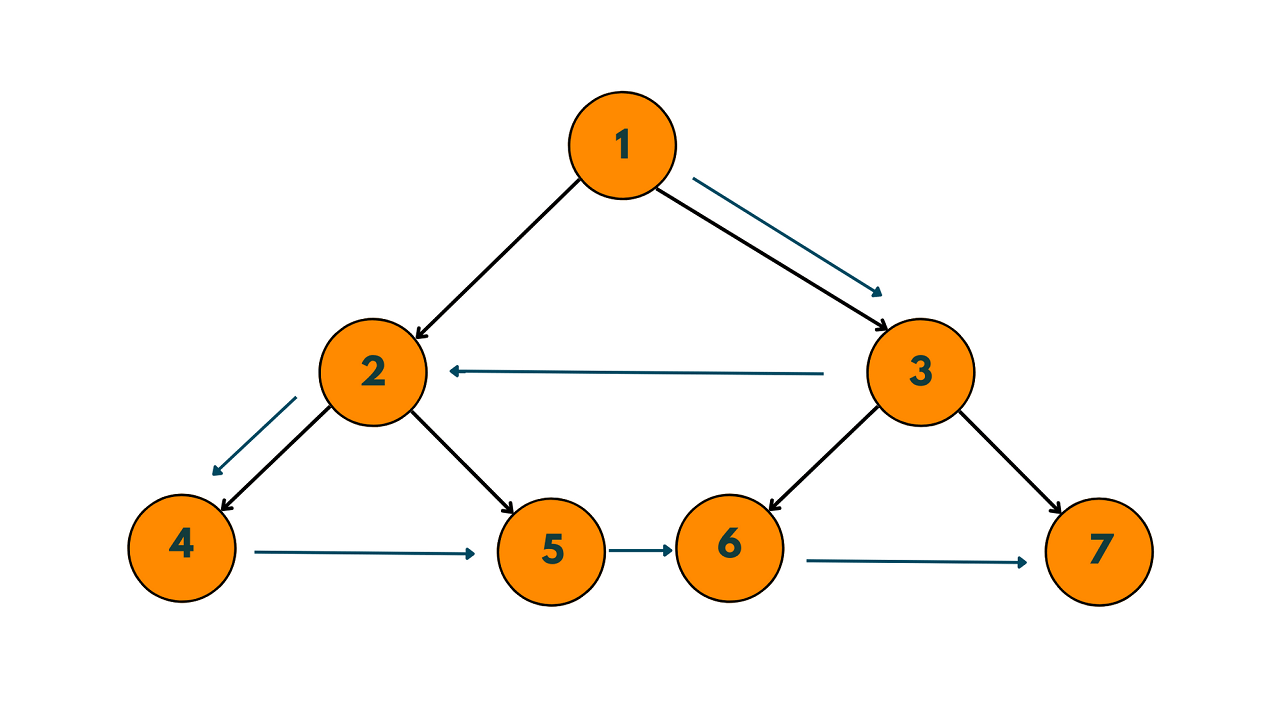
The Zig-zag traversal of a binary tree is a variation of the level-order traversal algorithm. In level-order traversal, we visit all the nodes of a level from left to right and then move on to the next level. In zig-zag traversal, we visit the nodes of each level alternately from left to right and right to left.
Let's take a look at an example binary tree to understand the zig-zag traversal:
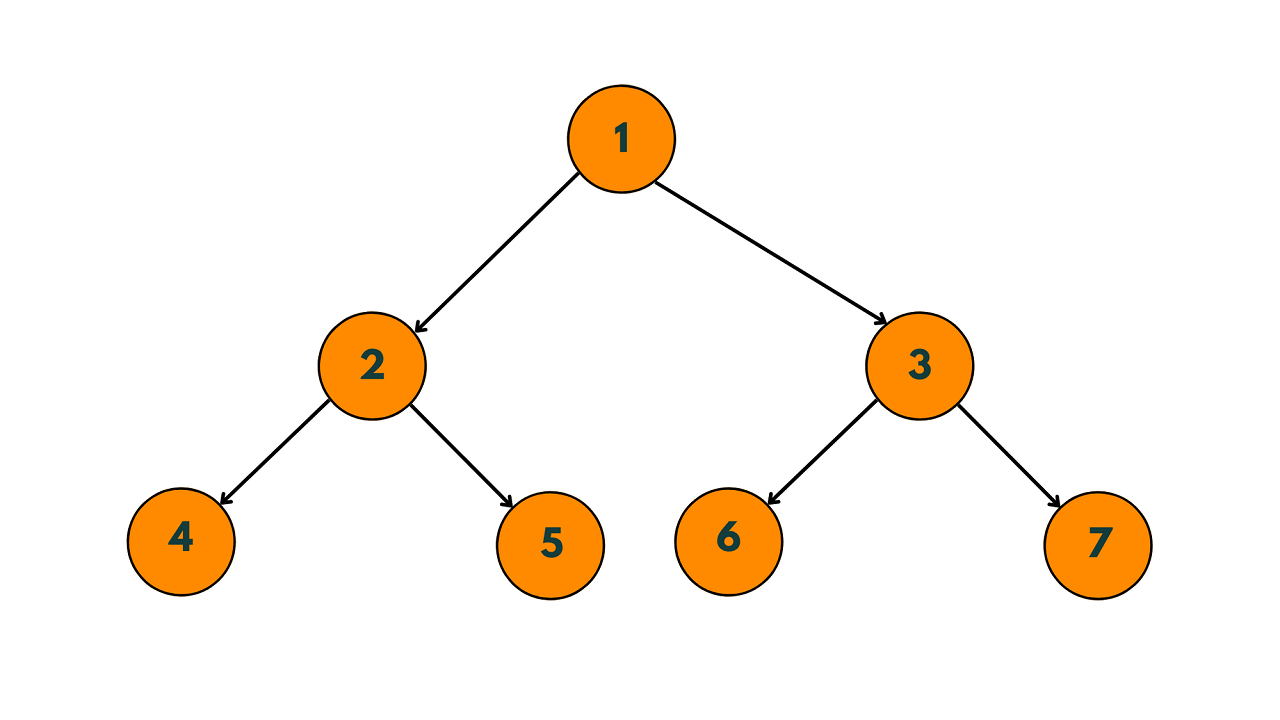
The zig-zag traversal of this binary tree would be: 1 3 2 4 5 6 7
There are several different approaches to implementing zigzag traversal of a binary tree. Here are four different approaches:
Method 1) Using Two Stacks
This approach involves using two stacks to keep track of the nodes of the current level and the next level. We alternate the direction of traversal between levels by toggling a boolean flag.
We push the children of a node onto the next level stack in the appropriate order based on the traversal direction. Once the current level stack is empty, we swap the stacks and continue the traversal.'
Here's the C++ code for the zig-zag traversal of a binary tree using two stacks:
#include<iostream> #include<stack> using namespace std; struct TreeNode { int val; TreeNode* left; TreeNode* right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; void zigzagTraversal(TreeNode* root) { if (!root) return; stack<TreeNode*> currentLevel; stack<TreeNode*> nextLevel; bool leftToRight = true; currentLevel.push(root); while (!currentLevel.empty()) { TreeNode* currentNode = currentLevel.top(); currentLevel.pop(); cout << currentNode->val << " "; if (leftToRight) { if (currentNode->left) nextLevel.push(currentNode->left); if (currentNode->right) nextLevel.push(currentNode->right); } else { if (currentNode->right) nextLevel.push(currentNode->right); if (currentNode->left) nextLevel.push(currentNode->left); } if (currentLevel.empty()) { leftToRight = !leftToRight; swap(currentLevel, nextLevel); } } } int main() { TreeNode* root = new TreeNode(1); root->left = new TreeNode(2); root->right = new TreeNode(3); root->left->left = new TreeNode(4); root->left->right = new TreeNode(5); root->right->left = new TreeNode(6); root->right->right = new TreeNode(7); zigzagTraversal(root); return 0; }
Output:
1 3 2 4 5 6 7
In the above code, we first check if the root node is NULL. If it is, we return from the function. Otherwise, we create two stacks - one for the current level and the other for the next level. We also initialize a boolean variable leftToRight to true, which indicates that we need to visit the nodes from left to right.
We then start a loop that runs until the current level stack is empty. In each iteration of the loop, we pop the top node from the current level stack and print its value. We also push its left and right children onto the next level stack in the appropriate order, depending on the value of leftToRight.
If the current level stack becomes empty, we swap the current level stack with the next level stack, toggle the value of leftToRight, and continue the loop.
Using two stacks is a more space-efficient way to implement zig-zag traversal than using a queue since we don't need to store all the nodes of a level in a separate container. Instead, we use two stacks to keep track of the current and next levels.
The time complexity of the zig-zag traversal of a binary tree using two stacks is O(N), where N is the number of nodes in the tree. This is because we need to visit each node of the binary tree exactly once to print its value.
Method 2) Using Deque
This approach involves using a deque (double-ended queue) to keep track of the nodes of the current level and the next level. We alternate the direction of traversal between levels by toggling a boolean flag.
We insert the children of a node into the deque based on the traversal direction. We pop the nodes from the front or the back of the deque based on the traversal direction. Once the deque is empty, we continue the traversal.
Here is the code to implement the zigzag traversal of a binary tree using a deque:
#include<iostream> #include<deque> using namespace std; struct Node { int val; Node* left; Node* right; Node(int v) : val(v), left(nullptr), right(nullptr) {} }; void zigzagTraversal(Node* root) { if (!root) { return; } deque<Node*> dq; dq.push_back(root); bool direction = true; // true: left-to-right, false: right-to-left while (!dq.empty()) { int levelSize = dq.size(); vector<int> levelNodes(levelSize); for (int i = 0; i < levelSize; i++) { if (direction) { Node* node = dq.front(); dq.pop_front(); levelNodes[i] = node->val; if (node->left) { dq.push_back(node->left); } if (node->right) { dq.push_back(node->right); } } else { Node* node = dq.back(); dq.pop_back(); levelNodes[i] = node->val; if (node->right) { dq.push_front(node->right); } if (node->left) { dq.push_front(node->left); } } } direction = !direction; for (int i = 0; i < levelSize; i++) { cout << levelNodes[i] << " "; } } } int main() { Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); root->right->left = new Node(6); root->right->right = new Node(7); cout << "Zigzag traversal: "; zigzagTraversal(root); cout << endl; return 0; }
Output:
Zigzag traversal: 1 3 2 4 5 6 7
In this implementation, we first push the root node onto the deque and initialize a boolean variable direction to keep track of the traversal direction. We set direction to true for the first level, which means we traverse the nodes from left to right.
We then enter a while loop that runs until the deque is empty. In each iteration of the loop, we get the size of the deque to determine the number of nodes in the current level. We initialize a vector levelNodes to store the nodes of the current level in the appropriate order based on the traversal direction.
We then iterate over each node in the current level and do the following:
- If the traversal direction is left-to-right, we pop a node from the front of the deque using
dq.front(), add its value tolevelNodes, and push its children onto the back of the deque usingdq.push_back(). - If the traversal direction is right-to-left, we pop a node from the back of the deque using
dq.back(), add its value tolevelNodes, and push its children onto the front of the deque usingdq.push_front().
Once we finish iterating over all nodes in the current level, we reverse the traversal direction by toggling the direction variable using !direction.
Finally, we iterate over levelNodes and print each node's value. We repeat this process until the deque is empty.
The time complexity of the zigzag traversal of a binary tree using deque is O(N), where N is the number of nodes in the tree. This is because we visit each node once and perform constant-time operations on it.
Method 3) Using Recursion
This approach involves using recursion to traverse the binary tree. We pass a level parameter to the recursive function that keeps track of the current level and the traversal direction. We traverse the left and right subtrees in the appropriate order based on the level and the traversal direction.
We print the value of the node when we visit it. Once we finish traversing the binary tree, we have the nodes of each level in separate vectors. We reverse the nodes of every other level and concatenate all the vectors to get the zigzag traversal.
Here is the C++ code to implement the zigzag traversal of a binary tree using recursion:
#include<iostream> using namespace std; struct Node { int val; Node* left; Node* right; Node(int v) : val(v), left(nullptr), right(nullptr) {} }; void zigzagTraversal(Node* root, int level, bool direction) { if (!root) { return; } if (level == 1) { cout << root->val << " "; } else if (level > 1) { if (direction) { zigzagTraversal(root->left, level - 1, direction); zigzagTraversal(root->right, level - 1, direction); } else { zigzagTraversal(root->right, level - 1, direction); zigzagTraversal(root->left, level - 1, direction); } } } int height(Node* root) { if (!root) { return 0; } int leftHeight = height(root->left); int rightHeight = height(root->right); return max(leftHeight, rightHeight) + 1; } void zigzagTraversal(Node* root) { if (!root) { return; } int h = height(root); bool direction = true; // true: left-to-right, false: right-to-left for (int i = 1; i <= h; i++) { zigzagTraversal(root, i, direction); direction = !direction; } } int main() { Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); root->right->left = new Node(6); root->right->right = new Node(7); cout << "Zigzag traversal: "; zigzagTraversal(root); cout << endl; return 0; }
Output:
Zigzag traversal: 1 3 2 4 5 6 7
In this implementation, we first define a helper function zigzagTraversal that takes the root node, the current level, and the traversal direction as arguments. This function recursively traverses the binary tree and prints the nodes of the current level in the appropriate order based on the traversal direction. The function is called in the zigzagTraversal function for each level of the tree.
We also define a helper function height that computes the height of the binary tree. This function is used to determine the number of levels in the tree and the order of traversal for each level.
In the zigzagTraversal function, we first compute the height of the tree using the height function. We then initialize a boolean variable direction to keep track of the traversal direction. We set direction to true for the first level, which means we traverse the nodes from left to right.
We then iterate over each level of the tree and call the zigzagTraversal function for the current level, passing in the root node, the level number, and the traversal direction. After each level, we reverse the traversal direction by toggling the direction variable using !direction.
The time complexity of the zigzag traversal of a binary tree using recursion is O(N^2), where N is the number of nodes in the tree. This is because we visit each node once and perform O(N) recursive calls, one for each level of the tree.
Conclusion
In conclusion, Zig-Zag Traversal is an interesting coding challenge you might face in your next technical interview. You now have 3 different methods in your arsenal to implement it.